题目内容
14. 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.(1)求证:BD=DC;
(2)若EC=1,CD=2,求⊙O的半径;
(3)若∠A=30°,连接DE,过点B作BF∥DE,交⊙O于点F,连接OF,则∠BOF的度数是90°.
分析 (1)连接BD,根据圆周角定理得到AD⊥BC,根据等腰三角形的性质证明即可;
(2)连接BE,根据圆周角定理、相似三角形的判定定理得到△BEC∽△ADC,根据相似三角形的性质列出比例式,计算即可;
(3)根据等腰三角形的性质得到∠ABC=∠C=75°,根据直角三角形的性质得到DE=DB,根据平行线的性质、等腰三角形的性质计算即可.
解答 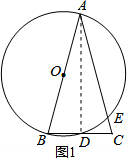 (1)证明:如图1,连接BD,
(1)证明:如图1,连接BD,
∵AB是⊙O的直径,
∴AD⊥BC,又AB=AC,
∴BD=DC;
(2)解: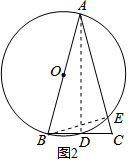 如图2,连接BE,
如图2,连接BE,
∵CD=2,
∴BC=2CD=4,
∵AB是⊙O的直径,
∴∠AEB=90°,又AD⊥BC,
∴△BEC∽△ADC,
∴$\frac{EC}{DC}$=$\frac{BC}{AC}$,即$\frac{1}{4}$=$\frac{4}{AC}$,
解得,AC=16,
∴⊙O的半径=$\frac{1}{2}$AB=$\frac{1}{2}$AC=8;
(3)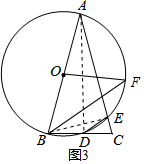 解:∵∠A=30°,
解:∵∠A=30°,
∴∠ABC=∠C=75°,
∴∠EBC=15°,
在Rt△BEC中,D为BC的中点,
∴DE=DB,
∴∠DEB=∠EBC=15°,
∵BF∥DE,
∴∠FBE=∠DEB=15°,
∴∠OBF=45°,又OB=OF,
∴∠BOF=90°,
故答案为:90°.
点评 本题考查的是圆周角定理、相似三角形的判定和性质的应用,掌握圆周角定理及其推论、灵活运用相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.若a、b为有理数,下列说法正确的是( )
| A. | 若a≠b,则a2≠b2 | B. | 若a2=b2,则a=b | ||
| C. | 若a>b,则a2>b2 | D. | 若a、b不全为零,则a2+b2>0 |
 如图,在△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法:
如图,在△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法: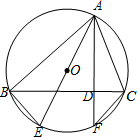 如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,弦AF与BC相交于点D,若BE=CF,求证:AF⊥BC.
如图,△ABC是⊙O的内接三角形,AE是⊙O的直径,弦AF与BC相交于点D,若BE=CF,求证:AF⊥BC.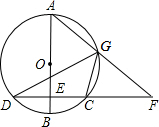 已知:如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,G是弧AC上的任意一点,AG、DC的延长线相交于点F.
已知:如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,G是弧AC上的任意一点,AG、DC的延长线相交于点F.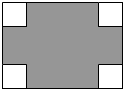 在长为8cm、宽为5cm的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.
在长为8cm、宽为5cm的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长. 将连续的奇数1,3,5,7,9…,排成如下的数表:
将连续的奇数1,3,5,7,9…,排成如下的数表: