题目内容
3.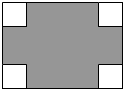 在长为8cm、宽为5cm的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.
在长为8cm、宽为5cm的矩形的四个角上分别截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.
分析 等量关系为:矩形面积-四个全等的小正方形面积=矩形面积×80%,列方程即可求解.
解答 解:设小正方形的边长为xcm,由题意得
8×5-4x2=80%×5×8,
40-4x2=32,
4x2=8,
x2=2.
解得:x1=$\sqrt{2}$,x2=-$\sqrt{2}$,
经检验x1=$\sqrt{2}$符合题意,x2=-$\sqrt{2}$不符合题意,舍去;
所以x=$\sqrt{2}$.
答:截去的小正方形的边长为$\sqrt{2}$cm.
点评 此题考查了一元二次方程的应用,读懂题意,找到合适的等量关系是解决本题的关键,实际问题中需注意负值应舍去.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E.
如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E. 如图,在△ABC中,∠B=∠C,AB=10cm,BC=8cm,D为AB的中点,点P在线段上以3cm/s 的速度由点B向点C运动,同时,点Q在线段CA上以相同速度由点C向点A运动,一个点到达终点后另一个点也停止运动.当△BPD与△CQP全等时,求点P运动的时间.
如图,在△ABC中,∠B=∠C,AB=10cm,BC=8cm,D为AB的中点,点P在线段上以3cm/s 的速度由点B向点C运动,同时,点Q在线段CA上以相同速度由点C向点A运动,一个点到达终点后另一个点也停止运动.当△BPD与△CQP全等时,求点P运动的时间. 如图,O为坐标原点,四边形OABC为矩形,A(20,0),C(0,6),点D是OA的中点,点P在BC上运动,当△ODP是等腰三角形时,则P点的坐标为P1(2,6),P2(5,6),P3(8,6),P4(18,6).
如图,O为坐标原点,四边形OABC为矩形,A(20,0),C(0,6),点D是OA的中点,点P在BC上运动,当△ODP是等腰三角形时,则P点的坐标为P1(2,6),P2(5,6),P3(8,6),P4(18,6).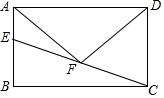 已知:如图,在矩形ABCD中,点E在边AB上,点F为CE的中点,连接AF、DF.
已知:如图,在矩形ABCD中,点E在边AB上,点F为CE的中点,连接AF、DF.