题目内容
19．
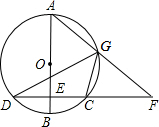已知：如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，G是弧AC上的任意一点，AG、DC的延长线相交于点F．求证：∠FGC=∠AGD．
分析 连接AD，根据垂径定理得到$\widehat{AD}$=$\widehat{AC}$，根据圆周角定理得到∠ADC=∠AGD，根据圆内接四边形的性质证明即可．
解答 
证明：连接AD，
∵弦CD⊥AB，
∴$\widehat{AD}$=$\widehat{AC}$，
∴∠ADC=∠AGD，
∵四边形ADCG是圆内接四边形，
∴∠ADC=∠FGC，
∴∠FGC=∠AGD．
点评 本题考查的是圆周角定理和垂径定理的应用，掌握圆周角定理、垂径定理是解题的关键．
练习册系列答案
相关题目
9．下面条件中，不能证出Rt△ABC≌Rt△A'B'C'的是（ ）
| A． | AC=A'C'，BC=B'C' | B． | AB=A'B'，AC=A'C' | C． | AB=B'C'，AC=A'C' | D． | ∠B=∠B'，AB=A'B' |
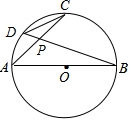已知：如图AB为⊙O的直径，弦AC、BD相交于点P，
如图，△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，交AC于点E．
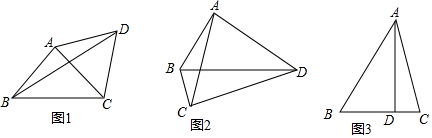
如图，O为坐标原点，四边形OABC为矩形，A（20，0），C（0，6），点D是OA的中点，点P在BC上运动，当△ODP是等腰三角形时，则P点的坐标为P1（2，6），P2（5，6），P3（8，6），P4（18，6）．