Question

6．如图，边长为6的等边三角形ABC中，E是对称轴AD上的一个动点，连接EC，将线段EC绕点C逆时针转60°得到FC，连接DF．则在点E运动过程中，DF的最小值是（　　）

• A． 6
• B． 3
• C． 2
• D． 1.5

Answer 1

分析 取线段AC的中点G，连接EG，根据等边三角形的性质以及角的计算即可得出CD=CG以及∠FCD=∠ECG，由旋转的性质可得出EC=FC，由此即可利用全等三角形的判定定理SAS证出△FCD≌△ECG，进而即可得出DF=GE，再根据点G为AC的中点，即可得出EG的最小值，此题得解．

解答 解：取线段AC的中点G，连接EG，如图所示．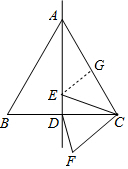
∵△ABC为等边三角形，且AD为△ABC的对称轴，
∴CD=CG=$\frac{1}{2}$AB=3，∠ACD=60°，
∵∠ECF=60°，
∴∠FCD=∠ECG．
在△FCD和△ECG中，$\left\{\begin{array}{l}{FC=EC}\\{∠FCD=∠ECG}\\{DC=GC}\end{array}\right.$，
∴△FCD≌△ECG（SAS），
∴DF=GE．
当EG∥BC时，EG最小，
∵点G为AC的中点，
∴此时EG=DF=$\frac{1}{2}$CD=$\frac{3}{2}$．
故选D．

点评 本题考查了等边三角形的性质以及全等三角形的判定与性质，解题的关键是通过全等三角形的性质找出DF=GE．本题属于中档题，难度不大，解决该题型题目时，根据全等三角形的性质找出相等的边是关键．