��Ŀ����
11�� ������֪��������x��y����x+y=7����$\sqrt{{x}^{2}+4}$+$\sqrt{{y}^{2}+9}$����СֵΪ$\sqrt{74}$����ʱx��ֵΪ$\frac{14}{5}$������ʾ�����������������ϵ���Ϳ��Դ����ν�ϵĽǶ�����$\sqrt{{x}^{2}+4}$���������$\sqrt{{3}^{2}+{4}^{2}}$�����߳�Ϊ3��4��ֱ�������ε�б�ߣ���
������֪��������x��y����x+y=7����$\sqrt{{x}^{2}+4}$+$\sqrt{{y}^{2}+9}$����СֵΪ$\sqrt{74}$����ʱx��ֵΪ$\frac{14}{5}$������ʾ�����������������ϵ���Ϳ��Դ����ν�ϵĽǶ�����$\sqrt{{x}^{2}+4}$���������$\sqrt{{3}^{2}+{4}^{2}}$�����߳�Ϊ3��4��ֱ�������ε�б�ߣ���������ͼ����ÿ���߳�Ϊ1�������������У���A��B���ڸ���ϣ���AB=7���������߶�AB���ҵ�һ��P��ʹAP�ij�Ϊ�����������x��
���� ����ͼ��������ֱ�������Σ���ACP�͡�BDP��������C����AB�ĶԳƵ�C�䣬��������֮�䣬�߶���̿�֪$\sqrt{{x}^{2}+4}$+$\sqrt{{y}^{2}+9}$����Сֵ�����߶�C��D�ij���������ƽ���������x��ֵ��
���  �⣺��I����A��B����ֱ���AB�Ĵ���AC��BD����AC=2��BD=3��
�⣺��I����A��B����ֱ���AB�Ĵ���AC��BD����AC=2��BD=3��
����C����AB�ĶԳƵ�C�䣬����C��D��AB��P������CP��
��CP=C��P��
��AP=x��BP=y����y=7-x��
�ɹ��ɶ����ã�CP=$\sqrt{{x}^{2}+4}$��PD=$\sqrt{{y}^{2}+9}$��
���ʱ$\sqrt{{x}^{2}+4}$+$\sqrt{{y}^{2}+9}$��ֵ��С��
��C��D=C��P+DP=CP+DP=$\sqrt{{x}^{2}+4}$+$\sqrt{{y}^{2}+9}$=$\sqrt{{7}^{2}+��3+2��^{2}}$=$\sqrt{74}$��
��AC���AB��BD��AB��
��AC���BD��
���APC��ס�BPD��
��$\frac{AP}{PB}=\frac{AC��}{BD}$��
��$\frac{x}{7-x}=\frac{2}{3}$��
��x=$\frac{14}{5}$��
�ʴ�Ϊ��$\sqrt{74}$��$\frac{14}{5}$��
��II����ͼ��ʾ��AP�ij������������x��
���� ��������ԳƵ����·�����⣬���������ǣ���ijһ��ĶԳƵ㣬����һ�������������ɵ��߶γ�������̾��룬ͨ�����ù��ɶ������������

 ��ͼ���������ABCDE�У���A+��B+��E=����DP��CP�ֱ�ƽ�֡�EDC����BCD�����P�Ķ����ǣ�������
��ͼ���������ABCDE�У���A+��B+��E=����DP��CP�ֱ�ƽ�֡�EDC����BCD�����P�Ķ����ǣ�������| A�� | $\frac{1}{2}$��-90�� | B�� | 90��$+\frac{1}{2}��$ | C�� | $\frac{1}{2}��$ | D�� | 540��$-\frac{1}{2}��$ |
 ��ͼ���߳�Ϊ6�ĵȱ�������ABC�У�E�ǶԳ���AD�ϵ�һ�����㣬����EC�����߶�EC�Ƶ�C��ʱ��ת60��õ�FC������DF�����ڵ�E�˶������У�DF����Сֵ�ǣ�������
��ͼ���߳�Ϊ6�ĵȱ�������ABC�У�E�ǶԳ���AD�ϵ�һ�����㣬����EC�����߶�EC�Ƶ�C��ʱ��ת60��õ�FC������DF�����ڵ�E�˶������У�DF����Сֵ�ǣ�������| A�� | 6 | B�� | 3 | C�� | 2 | D�� | 1.5 |
| A�� | 0��m��1 | B�� | 1��m��2 | C�� | 2��m��3 | D�� | 3��m��4 |
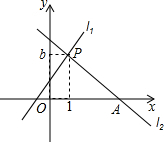 ��ͼ��ֱ��l1��y=x+1��ֱ��l2��y=mx+n���ڵ�P��1��b����ֱ��l2��x�ύ�ڵ�A��4��0����
��ͼ��ֱ��l1��y=x+1��ֱ��l2��y=mx+n���ڵ�P��1��b����ֱ��l2��x�ύ�ڵ�A��4��0���� ��1����������߳�Ϊ1�������������л�һ���۽ǡ�ABC��ʹAB=$\sqrt{10}$��
��1����������߳�Ϊ1�������������л�һ���۽ǡ�ABC��ʹAB=$\sqrt{10}$��