题目内容
13.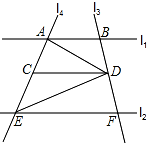 直线l1∥l2,直线l3与l1,l2,分别交于点B,F,直线l4与l1,l2分别交于点A,E,点D是直线l3上一动点,DC∥AB交l4于点C.
直线l1∥l2,直线l3与l1,l2,分别交于点B,F,直线l4与l1,l2分别交于点A,E,点D是直线l3上一动点,DC∥AB交l4于点C.(1)如图,当点D在l1、l2两线之间运动时,试找出∠BAD、∠DEF、∠ADE之间的等量关系,并说明理由;
(2)当点D在l1、l2两线上方运动时,试探究∠BAD、∠DEF、∠ADE之间的等量关系(点D和B、F不重合),画出图形,直接写出出结论.
分析 (1)由AB∥CD,根据平行线的性质得到∠BAD=∠ADC,而l1∥l2,则CD∥EF,得到∠DEF=∠CDE,于是∠BAD+DEF=∠ADE;
(2)当点D在FB的延长线上运动时(如图2),∠DEF=∠ADE+∠BAD,由两直线平行同位角相等可得:∠1=∠DEF,然后由外角的性质可得:∠1=∠BAD+∠ADE,进而可得:∠DEF=∠BAD+∠ADE,即:∠DEF-∠BAD=∠ADE.
解答 解:(1)∠BAD+∠DEF=∠ADE
理由如下,
∵AB∥CD,
∴∠BAD=∠ADC(两直线平行,内错角相等),
∵l1∥l2,DC∥AB,
∴CD∥EF,
∴∠DEF=∠CDE(两直线平行,内错角相等),
故∠BAD+∠DEF=∠ADC+∠CDE.
即∠BAD+DEF=∠ADE;
(2)如图(2)所示,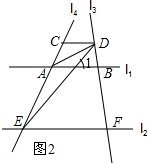
∠DEF-∠BAD=∠ADE.
理由:∵AB∥EF,
∴∠1=∠DEF,
∵∠1=∠BAD+∠ADE,
∴∠DEF=∠BAD+∠ADE,
即:∠DEF-∠BAD=∠ADE.
点评 本题考查了平行线的性质与判断,解题的关键是:熟记两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.

练习册系列答案
相关题目
4.已知点A的坐标为(a,b),O为坐标原点,连结OA,将线段OA绕点O按逆时针方向旋转180°得OA1,则点A1的坐标为( )
| A. | (-a,b) | B. | (a,-b) | C. | (-a,-b) | D. | (b,-a) |
2.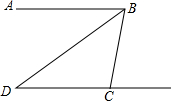 如图,AB∥CD,BD平分∠ABC,若∠DCB=100°,则∠D的度数是( )
如图,AB∥CD,BD平分∠ABC,若∠DCB=100°,则∠D的度数是( )
 如图,AB∥CD,BD平分∠ABC,若∠DCB=100°,则∠D的度数是( )
如图,AB∥CD,BD平分∠ABC,若∠DCB=100°,则∠D的度数是( )| A. | 40° | B. | 50° | C. | 30° | D. | 45° |
 为缓解实验北校“停车难”问题,现计划拟建造地下停车库,建筑师提供了地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,其中AB=10m,BC=0.5m,为在入口标明限高,请你根据该图计算出停车库的限高.(精确到0.1m)
为缓解实验北校“停车难”问题,现计划拟建造地下停车库,建筑师提供了地下停车库的设计示意图,按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,其中AB=10m,BC=0.5m,为在入口标明限高,请你根据该图计算出停车库的限高.(精确到0.1m) 在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的⊙P过点C,若C的坐标为(0,2),AB=5,经过A、B、C三点的抛物线为y=ax2+bx+c.
在平面直角坐标系中△ABC的边AB在x轴上,且OA>OB,以AB为直径的⊙P过点C,若C的坐标为(0,2),AB=5,经过A、B、C三点的抛物线为y=ax2+bx+c.