题目内容
8.设a为无理数,n为整数,我们定义:当|n-a|<|n+1-a|时,称a靠近n.例如:因为|1-$\sqrt{2}$|<|2-$\sqrt{2}$|,|1-$\sqrt{3}$|>|2-$\sqrt{3}$|,$\sqrt{2}$靠近1,$\sqrt{3}$靠近2.利用计算器探究:(1)在$\sqrt{5}$,$\sqrt{6}$,$\sqrt{7}$,$\sqrt{8}$中哪些靠近2?哪些靠近3?
(2)在$\sqrt{10}$,$\sqrt{11}$,$\sqrt{12}$,$\sqrt{13}$,$\sqrt{14}$,$\sqrt{15}$中哪些靠近3?哪些靠近4?
(3)在$\sqrt{17}$,$\sqrt{18}$,$\sqrt{19}$,$\sqrt{20}$,$\sqrt{21}$,$\sqrt{22}$,$\sqrt{23}$中哪些靠近4?哪些靠近5?
(4)猜测:在$\sqrt{{n}^{2}+1}$,$\sqrt{{n}^{2}+2}$,$\sqrt{{n}^{2}+3}$,…,$\sqrt{(n+1)^{2}-1}$共有多少个无理数?其中多少个靠近n?(友情提示:$\sqrt{(n+1)^{2}-1}$=$\sqrt{{n}^{2}+2n}$)
分析 根据我们定义:当|n-a|<|n+1-a|时,称a靠近n,估算出无理数的范围,进行逐一分析,即可解答.
解答 解:(1)∵|2-$\sqrt{5}$|<|3-$\sqrt{5}$|,|2-$\sqrt{6}$|<|3-$\sqrt{6}$|,|2-$\sqrt{7}$|>|3-$\sqrt{7}$|,|2-$\sqrt{8}$|>|3-$\sqrt{8}$|,
∴$\sqrt{5}$,$\sqrt{6}$接近2,$\sqrt{7}$,$\sqrt{8}$接近3;
(2)∵|3-$\sqrt{10}$|<|4-$\sqrt{10}$|,|3-$\sqrt{11}$|<|4-$\sqrt{11}$|,|3-$\sqrt{12}$|<|4-$\sqrt{12}$|,|3-$\sqrt{13}$|>|4-$\sqrt{13}$|,|3-$\sqrt{14}$|>|4-$\sqrt{14}$|,|3-$\sqrt{15}$|>|4-$\sqrt{15}$|,
∴$\sqrt{10}$,$\sqrt{11}$,$\sqrt{12}$接近3,$\sqrt{13},\sqrt{14}$,$\sqrt{15}$接近4;
(3)∵|4-$\sqrt{17}$|<|5-$\sqrt{17}$|,|4-$\sqrt{18}$|<|5-$\sqrt{18}$|,|4-$\sqrt{19}$|<|5-$\sqrt{19}$|,|4-$\sqrt{20}$|<|5-$\sqrt{20}$|,
∴$\sqrt{17}$,$\sqrt{18}$,$\sqrt{19}$,$\sqrt{20}$接近4,
∵|4-$\sqrt{21}$|>|5-$\sqrt{21}$|,|4-$\sqrt{22}$|>|5-$\sqrt{22}$|,|4-$\sqrt{23}$|>|5-$\sqrt{23}$|,|4-$\sqrt{24}$|>|5-$\sqrt{24}$|,
∴$\sqrt{21}$,$\sqrt{22}$,$\sqrt{23}$,$\sqrt{24}$接近5;
(4)根据以上规律,猜测:共有2n个无理数,其中n个接近n.
点评 本题考查了估算无理数的大小,解决本题的关键是明确定义:当|n-a|<|n+1-a|时,称a靠近n.

 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案| A. | (3,-4) | B. | (2,-3) | C. | (-3,2) | D. | (4,-3) |
| A. | 9.7×10-7 | B. | 97×10-7 | C. | 0.97×10-7 | D. | 9.7×10-8 |
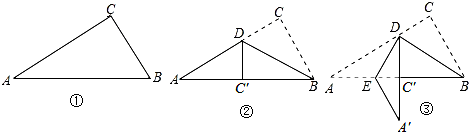
| A. | $2\sqrt{2}$cm | B. | $2\sqrt{3}$cm | C. | $\frac{8}{3}$cm | D. | 3cm |
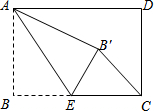 如图,长方形的宽AB=3,长BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.
如图,长方形的宽AB=3,长BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.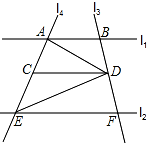 直线l1∥l2,直线l3与l1,l2,分别交于点B,F,直线l4与l1,l2分别交于点A,E,点D是直线l3上一动点,DC∥AB交l4于点C.
直线l1∥l2,直线l3与l1,l2,分别交于点B,F,直线l4与l1,l2分别交于点A,E,点D是直线l3上一动点,DC∥AB交l4于点C.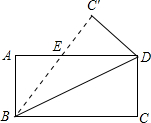 如图,将长方形纸片ABCD沿对角线BD折叠,使点C落在C′处,BC′交AD于E.若∠DBC=22.5°,则在不添加任何辅助线的情况下,图中45°的角(虚线也视为角的边)有( )
如图,将长方形纸片ABCD沿对角线BD折叠,使点C落在C′处,BC′交AD于E.若∠DBC=22.5°,则在不添加任何辅助线的情况下,图中45°的角(虚线也视为角的边)有( )