题目内容
5.某机械租赁公司有同一型号的机械设备40套,经过一段时间的经营发现,当每套设备的月租金为270元时,恰好全部租出,在此基础上,当每套设备的月租金每提高10元时,这种设备减少租出一套,且没租出的一套设备每月需支出费用(维护费、管理费等)20元,设每套设备的月租金为x(元),租赁公司出租该型号设备的月收益(收益=租金收入-支出费用)为y(元)(1)用含x的代数式表示未出租的设备数(套)以及所有未出租设备(套)的支出费用;
(2)当月租金分别为300元和350元时,租赁公司的月收益分别是多少元?此时应该出租多少套机械设备?请你简要说明理由;
(3)当x为何值时,租赁公司出租该型号设备的月收益最大?最大月收益为多少?
分析 (1)根据每套设备的月租金每提高10元时,这种设备减少租出一套,且没租出的一套设备每月需支出费用(维护费、管理费等)20元,列出相应的代数式即可;
(2)根据题意求出月租金分别为300元与350元时的月收益,以及出租的机械设备即可;
(3)表示出y与x的二次函数解析式,利用二次函数的性质求出y的最大值,以及此时x的值即可.
解答 解:(1)根据题意得:未出租的设备数为$\frac{x-270}{10}$套,所有未出租设备(套)的支出费用为20×$\frac{x-270}{10}$=2(x-270)元;
(2)当月租金为300元时,少租$\frac{300-270}{10}$=3套,公司收益为300×37-3×20=11040(元);
当月租金为350元时,少租$\frac{350-270}{10}$=8套,公司收益为350×32-8×20=11040(元),
此时应该出租32套,租金为300元,租出去有坏的风险;
(3)根据题意得:y=x(40-$\frac{x-270}{10}$)-$\frac{x-270}{10}$×20=-$\frac{1}{10}$x2+65x+540=-$\frac{1}{10}$(x-325)2+11102.5(x>270),
当x=325时,y最大为11102.5,
则x为325时,租赁公司出租该型号设备的月收益最大,最大月收益为11102.5元.
点评 此题考查了二次函数的应用,弄清关系“每套设备的月租金每提高10元时,这种设备减少租出一套”是解本题的关键.

练习册系列答案
相关题目
16.2014年初,埃博拉病毒疯狂袭击西非国家,随之蔓延至美国、西班牙等地,人们谈“埃”色变,2014所10月6日世界卫生组织发布公报说,埃博拉病毒(EBV)属丝状病毒科,长度为0.00000097米,将0.00000097用科学记数法表示为( )
| A. | 9.7×10-7 | B. | 97×10-7 | C. | 0.97×10-7 | D. | 9.7×10-8 |
20.如图①是一个直角三角形纸片,∠A=30°,BC=4cm,将其折叠,使点C落在斜边上的点C′处,折痕为BD,如图②,再将②沿DE折叠.使点A落在DC′的延长线上的点A′处,如图③,则折痕DE的长为( )
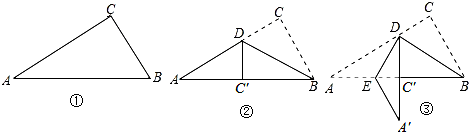

| A. | $2\sqrt{2}$cm | B. | $2\sqrt{3}$cm | C. | $\frac{8}{3}$cm | D. | 3cm |
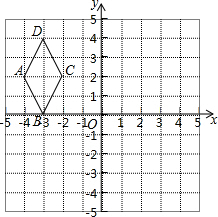 下面方格中有一个菱形ABCD和点O,请你在方格中画出以下图形(只要求画出平移、旋转后的图形,不要求写出作图步骤和过程).
下面方格中有一个菱形ABCD和点O,请你在方格中画出以下图形(只要求画出平移、旋转后的图形,不要求写出作图步骤和过程).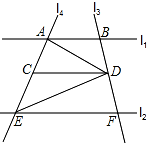 直线l1∥l2,直线l3与l1,l2,分别交于点B,F,直线l4与l1,l2分别交于点A,E,点D是直线l3上一动点,DC∥AB交l4于点C.
直线l1∥l2,直线l3与l1,l2,分别交于点B,F,直线l4与l1,l2分别交于点A,E,点D是直线l3上一动点,DC∥AB交l4于点C.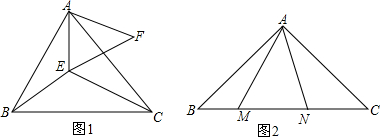
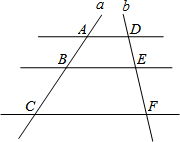 如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F,若AB=2,AC=6,DE=1.5,则DF的长为( )
如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F,若AB=2,AC=6,DE=1.5,则DF的长为( )