题目内容
1．
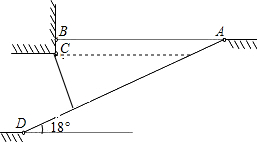为缓解实验北校“停车难”问题，现计划拟建造地下停车库，建筑师提供了地下停车库的设计示意图，按规定，地下停车库坡道口上方要张贴限高标志，以便告知停车人车辆能否安全驶入，其中AB=10m，BC=0.5m，为在入口标明限高，请你根据该图计算出停车库的限高．（精确到0.1m）（sin18°≈0.309，cos18°≈0.951，tan18°≈0.325）
分析 根据锐角三角函数的定义，可在Rt△ABM中解得BM的值，进而求得CM的值，在Rt△CME中，利用正弦的定义，即可求得CE的值．
解答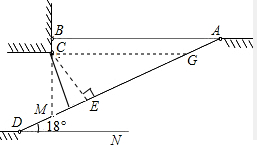 
解：在Rt△ABD中，∠BAD=18°，AB=10m，
∴BD=AB×tan18°≈3.25m，
∴CM=BM-BC=3.25-0.5=2.75m，
在Rt△CDE中，∠CME=72°，CD≈2.75m，
∴CE=CM×sin72°≈2.6m．
答：CE的高为2.6m．
点评 此题考查了解直角三角形的应用，用到的知识点是三角函数的定义，解题的关键是利用三角函数求出CM的长．
练习册系列答案
相关题目
11．
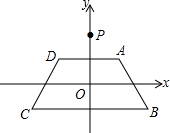如图，在平面直角坐标系xOy中，等腰梯形ABCD的顶点坐标分别为A（1，1），B（2，-1），C（-2，-1），D（-1，1）．y轴上一点P（0，2）绕点A旋转180°得点P1，点P1绕点B旋转180°得点P2，点P2绕点C旋转180°得点P3，点P3绕点D旋转180°得点P4，…，则点P2014的坐标是（ ）
如图，在平面直角坐标系xOy中，等腰梯形ABCD的顶点坐标分别为A（1，1），B（2，-1），C（-2，-1），D（-1，1）．y轴上一点P（0，2）绕点A旋转180°得点P1，点P1绕点B旋转180°得点P2，点P2绕点C旋转180°得点P3，点P3绕点D旋转180°得点P4，…，则点P2014的坐标是（ ）| A． | （2014，2） | B． | （2014，-2） | C． | （2012，-2） | D． | （2012，2） |
在如图的四边形MNOP中，证明：△PMO≌△NOM．
16．2014年初，埃博拉病毒疯狂袭击西非国家，随之蔓延至美国、西班牙等地，人们谈“埃”色变，2014所10月6日世界卫生组织发布公报说，埃博拉病毒（EBV）属丝状病毒科，长度为0.00000097米，将0.00000097用科学记数法表示为（ ）
| A． | 9.7×10-7 | B． | 97×10-7 | C． | 0.97×10-7 | D． | 9.7×10-8 |
如图所示，已知2015是第k行的数字，则k等于673．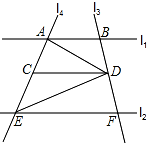
直线l1∥l2，直线l3与l1，l2，分别交于点B，F，直线l4与l1，l2分别交于点A，E，点D是直线l3上一动点，DC∥AB交l4于点C．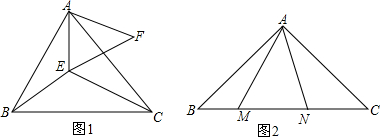
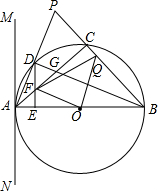如图，已知△ABP是等腰三角形，AB=BP，以AB为直径的⊙O交AP于点D，交BP于点C，连接BD交AC于点G，直线MN过点A，且∠PAM=$\frac{1}{2}$∠ABP．