题目内容
6.一艘轮船航行在A处时,港口C正好在它的东北方向,如果按东北方向行驶到港口,会遇到暗礁,为了避开暗礁,船只能向正东方向行驶到10千米的B处,在B处测得港口C在北偏东30°,求:此时船离港口C的距离.分析 根据题意和特殊角的三角函数值可以求得BD和CD的长,从而可以求得BC的长,本题得以解决.
解答  解:如右图所示,CD⊥AB于点D,
解:如右图所示,CD⊥AB于点D,
由题意可得,∠ACD=45°,∠BCD=30°,AB=10,
∵tan∠ACD=$\frac{AD}{CD}$,tan∠BCD=$\frac{BD}{CD}$,
∴1=$\frac{AD}{CD}=\frac{AB+BD}{CD}=\frac{10+BD}{CD}$,$\frac{\sqrt{3}}{3}=\frac{BD}{CD}$,
解得,
BD=5$\sqrt{3}$+5,CD=15+5$\sqrt{3}$,
∴BC=$\sqrt{B{D}^{2}+C{D}^{2}}$=10$\sqrt{3}$+10,
即此时船离港口C的距离是(10$\sqrt{3}$+10)千米.
点评 本题考查解直角三角形的应用-方向角问题、勾股定理,解答本题的关键是明确题意,画出相应的图形,利用锐角三角函数和勾股定理解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.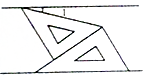 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
 如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )
如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )| A. | 15° | B. | 22.5° | C. | 30° | D. | 45° |
15.关于x的方程2x2+mx+n=0的两个根是-2和1,则nm的值为( )
| A. | -8 | B. | 8 | C. | 16 | D. | -16 |
 如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是同位角相等,两直线平行.
如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法,其理由是同位角相等,两直线平行.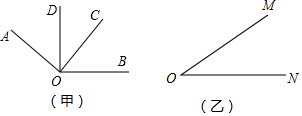
 如图,斜坡AC的坡比为0.8:1,若BC=5,则斜坡AC=$\sqrt{41}$.
如图,斜坡AC的坡比为0.8:1,若BC=5,则斜坡AC=$\sqrt{41}$. 已知,如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空).
已知,如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空).