题目内容
15.若关于x的分式方程$\frac{mx}{x-3}$-2=$\frac{1}{3-x}$无解,则m的值为2或-$\frac{1}{3}$.分析 先将分式方程化为整式方程,得出m的值,然后根据分式方程无实数根,分两种情况进行讨论,即可求出m的值.
解答 解:$\frac{mx}{x-3}$-2=$\frac{1}{3-x}$,
$\frac{mx}{x-3}$-$\frac{1}{3-x}$=2,
$\frac{mx+1}{x-3}$=2,
mx+1=2x-6,
即(m-2)x=-7,
当m-2=0时,整式方程无解,
即当m=2时,分式方程无解;
当m-2≠0时,根据分式方程无实数解,可得x=3,
∴3(m-2)=-7,
解得m=-$\frac{1}{3}$;
综上所述,当m=2或-$\frac{1}{3}$时,分式方程无解.
故答案为:2或-$\frac{1}{3}$.
点评 本题考查分式方程的解,熟记分式方程无解的条件是:去分母后所得整式方程无解,或解这个整式方程得到的解使原方程的分母等于0是解题的关键.

练习册系列答案
相关题目
6.一艘轮船航行在A处时,港口C正好在它的东北方向,如果按东北方向行驶到港口,会遇到暗礁,为了避开暗礁,船只能向正东方向行驶到10千米的B处,在B处测得港口C在北偏东30°,求:此时船离港口C的距离.
3.已知四边形的四条边长分别是a,b,c,d,其中a,b为对边,并且满足a2+b2+c2+d2=2ab+2cd,则这个四边形是( )
| A. | 任意四边形 | B. | 平行四边形 | ||
| C. | 对角线相等的四边形 | D. | 对角线垂直的四边形 |
10.若点p(x,y)是第四象限内的点,且点P到x轴的距离3,到y轴的距离2,则点P的坐标是( )
| A. | (2,-3) | B. | (-3,2) | C. | (-2,3) | D. | (3,-2) |
20.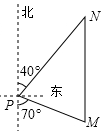 如图,一艘渔船位于钓鱼岛P的南偏东70°的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于钓鱼岛P的北偏东40°的N处,则N处与钓鱼岛P的距离为( )
如图,一艘渔船位于钓鱼岛P的南偏东70°的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于钓鱼岛P的北偏东40°的N处,则N处与钓鱼岛P的距离为( )
 如图,一艘渔船位于钓鱼岛P的南偏东70°的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于钓鱼岛P的北偏东40°的N处,则N处与钓鱼岛P的距离为( )
如图,一艘渔船位于钓鱼岛P的南偏东70°的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于钓鱼岛P的北偏东40°的N处,则N处与钓鱼岛P的距离为( )| A. | 40海里 | B. | 60海里 | C. | 70海里 | D. | 80海里 |
5.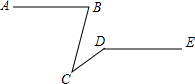 如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )
如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )
 如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )
如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )| A. | 20° | B. | 30° | C. | 40° | D. | 70° |
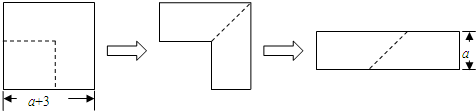
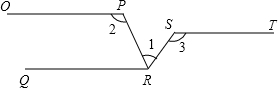 如图,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1=40°.
如图,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1=40°.