题目内容
11.如图(甲),∠AOC和∠BOD都是直角.(1)如果∠DOC=90°,∠AOB的度数是150度.
(2)找出图(甲)中和∠AOD相等的角,并说明相等的理由.
(3)在图(乙)中利用能够画出直角的工具再画一个与∠MON相等的角(请标出图中所画的直角,并写出这个与∠MON相等的角)
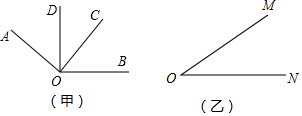
分析 (1)根据∠AOC=90°,∠DOC=30°,求出∠AOD的度数,然后即可求出∠AOB的度数;
(2)根据余角的性质可得图(甲)中和∠AOD相等的角;
(3)首先以ON为边,在∠NOM外画∠NOD=90°,再以OM为边在∠MOD外画∠AOM=90°,即可得到∠AOD=∠MON.
解答  解:(1)∵∠AOC=∠DOB=90°,∠DOC=30°,
解:(1)∵∠AOC=∠DOB=90°,∠DOC=30°,
∴∠AOD=90°-30°=60°,
∴∠AOB=90°+60°=150°.
(2)图(甲)中和∠AOD相等的角是∠BOC,同角的余角相等(或见下面解释)
∵∠AOC=∠DOB=90°,
∴∠AOD+∠DOC=∠BOC+∠DOC,
∴∠AOD=∠BOC;
(3)如图所示:
∵∠AOD+∠DOM=∠DOM+∠MON,
∴∠AOD=∠MON.
点评 本题考查了余角和补角,以及角的计算,解决本题的关键是熟记余角和补角的定义.

练习册系列答案
相关题目
19.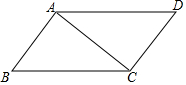 如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
 如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )
如图,在?ABCD中,连结AC,∠ABC=∠CAD=45°,AB=2,则BC的长是( )| A. | $\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 4 |
6.一艘轮船航行在A处时,港口C正好在它的东北方向,如果按东北方向行驶到港口,会遇到暗礁,为了避开暗礁,船只能向正东方向行驶到10千米的B处,在B处测得港口C在北偏东30°,求:此时船离港口C的距离.
16.已知a<b,下列四个不等式中正确的是( )
| A. | 3a>3b | B. | -a<-b | C. | a+3<b+3 | D. | a-6>b-6 |
3.已知四边形的四条边长分别是a,b,c,d,其中a,b为对边,并且满足a2+b2+c2+d2=2ab+2cd,则这个四边形是( )
| A. | 任意四边形 | B. | 平行四边形 | ||
| C. | 对角线相等的四边形 | D. | 对角线垂直的四边形 |
20.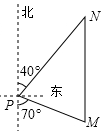 如图,一艘渔船位于钓鱼岛P的南偏东70°的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于钓鱼岛P的北偏东40°的N处,则N处与钓鱼岛P的距离为( )
如图,一艘渔船位于钓鱼岛P的南偏东70°的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于钓鱼岛P的北偏东40°的N处,则N处与钓鱼岛P的距离为( )
 如图,一艘渔船位于钓鱼岛P的南偏东70°的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于钓鱼岛P的北偏东40°的N处,则N处与钓鱼岛P的距离为( )
如图,一艘渔船位于钓鱼岛P的南偏东70°的M处,它以每小时40海里的速度向正北方向航行,2小时后到达位于钓鱼岛P的北偏东40°的N处,则N处与钓鱼岛P的距离为( )| A. | 40海里 | B. | 60海里 | C. | 70海里 | D. | 80海里 |
 将形状、大小完全相同的两个等腰三角形如图所示放置,点D在AB边上,△DEF绕点D旋转,腰DF和底边DE分别交△CAB的两腰CA,CB于M,N两点,若CA=5,AB=6,AD:AB=1:3,则MD+$\frac{12}{MA•DN}$的最小值为2$\sqrt{3}$.
将形状、大小完全相同的两个等腰三角形如图所示放置,点D在AB边上,△DEF绕点D旋转,腰DF和底边DE分别交△CAB的两腰CA,CB于M,N两点,若CA=5,AB=6,AD:AB=1:3,则MD+$\frac{12}{MA•DN}$的最小值为2$\sqrt{3}$. 随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,在水池中心竖直安装了一根高为2米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为1米处达到最高,水柱落地处离池中心3米.
随着新农村的建设和旧城的改造,我们的家园越来越美丽,小明家附近广场中央新修了个圆形喷水池,在水池中心竖直安装了一根高为2米的喷水管,它喷出的抛物线形水柱在与池中心的水平距离为1米处达到最高,水柱落地处离池中心3米.