题目内容
16. 已知,如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空).
已知,如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空).解:∵∠BAE+∠AED=180°(已知)
∴AB∥CD(同旁内角互补,两直线平行)
∴∠BAE=∠CEA( 两直线平行,内错角相等 )
又∵∠1=∠2
∴∠BAE-∠1=∠AEC-∠2即∠MAE=∠NEA
∴AM∥NE (内错角相等,两直线平行)
∴∠M=∠N (两直线平行,内错角相等).
分析 先根据平行线的判定,得到AB∥CD,再根据平行线的性质,得出∠MAE=∠NEA,进而得出AM∥NE,最后根据平行线的性质即可得到结论.
解答 解:∵∠BAE+∠AED=180°(已知)
∴AB∥CD(同旁内角互补,两直线平行)
∴∠BAE=∠CEA( 两直线平行,内错角相等 )
又∵∠1=∠2
∴∠BAE-∠1=∠AEC-∠2,即∠MAE=∠NEA
∴AM∥NE (内错角相等,两直线平行)
∴∠M=∠N (两直线平行,内错角相等)
故答案为:CD,同旁内角互补,两直线平行,∠CEA,∠NEA,AM,内错角相等,两直线平行,两直线平行,内错角相等.
点评 本题主要考查了平行线的性质与判定的运用,解题时注意:平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
相关题目
6.一艘轮船航行在A处时,港口C正好在它的东北方向,如果按东北方向行驶到港口,会遇到暗礁,为了避开暗礁,船只能向正东方向行驶到10千米的B处,在B处测得港口C在北偏东30°,求:此时船离港口C的距离.
5.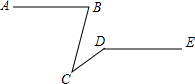 如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )
如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )
 如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )
如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )| A. | 20° | B. | 30° | C. | 40° | D. | 70° |
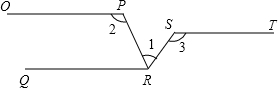 如图,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1=40°.
如图,OP∥QR∥ST,若∠2=100°,∠3=120°,则∠1=40°.
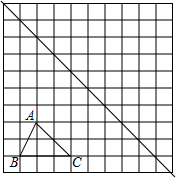 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)及直线l.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)及直线l.