题目内容
6.在Rt△ABC 中,∠ACB=90°,若D为AB的中点,CD=6,则AB的长为( )| A. | 24 | B. | 12 | C. | 6 | D. | 3 |
分析 根据直角三角形斜边上的中线等于斜边的一半解答.
解答 解:∵∠ACB=90°,D为AB的中点,
∴AB=2CD=12,
故选:B.
点评 本题考查的是直角三角形的性质,掌握直角三角形斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
7.在一个不透明的口袋里装着只有颜色不同的黑、白两种颜色的球共50只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复以上步骤,下表为实验的一组统计数据:
请估算口袋中白球的个数约为( )
| 摸球的次数n | 1000 | 1500 | 2000 | 5000 | 8000 | 10000 |
| 摸到白球的次数m | 582 | 960 | 1161 | 2954 | 4842 | 6010 |
| 摸到白球的频率 | 0.582 | 0.64 | 0.5805 | 0.5908 | 0.6053 | 0.601 |
| A. | 20 | B. | 25 | C. | 30 | D. | 35 |
11.函数y=(2m-1)x${\;}^{{m}^{2}-2}$是反比例函数,在第一象限内y随x的增大而减小,则m=( )
| A. | 1 | B. | -1 | C. | ±1 | D. | ±$\sqrt{3}$ |
15.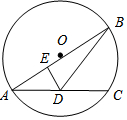 如图,AB是⊙O的直径,AC是⊙O的弦,D是AC的中点,过D作DE⊥AB于点E,连结BD.若AD=5,AE=4,则BD的长为( )
如图,AB是⊙O的直径,AC是⊙O的弦,D是AC的中点,过D作DE⊥AB于点E,连结BD.若AD=5,AE=4,则BD的长为( )
 如图,AB是⊙O的直径,AC是⊙O的弦,D是AC的中点,过D作DE⊥AB于点E,连结BD.若AD=5,AE=4,则BD的长为( )
如图,AB是⊙O的直径,AC是⊙O的弦,D是AC的中点,过D作DE⊥AB于点E,连结BD.若AD=5,AE=4,则BD的长为( )| A. | 2$\sqrt{15}$ | B. | $\sqrt{35}$ | C. | $\frac{5}{2}$$\sqrt{13}$ | D. | $\frac{7}{2}$$\sqrt{7}$ |
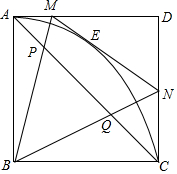 已知,在边长为4的正方形ABCD中,以AB为半径作扇形AOC,E是弧AC上一动点,过E作弧AC的切线分别交AD,CD于点M和N.
已知,在边长为4的正方形ABCD中,以AB为半径作扇形AOC,E是弧AC上一动点,过E作弧AC的切线分别交AD,CD于点M和N.