题目内容
14.“鄂尔多斯,温暖全世界”这句广告语及上乘的质量使鄂尔多斯的羊绒制品闻名中外,我市某羊绒企业的工厂店在销售中发现:某种羊绒围巾平均每天可售出100件,每件可获利80元;若售价减少10元,平均每天就可多售出20件;若想平均每天销售这种围巾盈利8400元,并使顾客得到更大的实惠,那么每件围巾应降价多少元?若想获利最大,应降价多少?分析 首先假设每件围巾应降价x元,即可得出(80-x)(100+$\frac{x}{10}$×20)=8400,即可求出x的值,进而得出y=(80-x)(100+2x)求出最值即可.
解答 解:设若想平均每天销售这种围巾盈利8400元,并使顾客得到更大的实惠,那么每件围巾应降价x元,根据题意得:
(80-x)(100+$\frac{x}{10}$×20)=8400,
解这个方程组得:
x1=10,x2=20,
为使顾客得到更大的实惠x=20;
答:想平均每天销售这种围巾盈利8400元,并使顾客得到更大的实惠,那么每件围巾应降价20元.
设:每件围巾应降价x元,设降价x元时,盈利为y元,则 y=(80-x)(100+$\frac{x}{10}$×20)0<x<80,
因为y=(80-x)(100+$\frac{x}{10}$×20),
=(80-x)(100+2x)
=8000+160x-100x-2x2
=-2x2+60x+8000
=-2(x-15)2+8450
所以当x=15时,y最大值=8450,
答:若想获利最大,应降价15元.
点评 此题主要考查了二次函数的最值问题以及一元二次方程的应用,根据已知得出二次函数的最值时是中考中考查重点,同学们应重点掌握.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
15.某校在“6•26国际禁毒日”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作如表频数分布表和频数分布直方图,请根据图表提供的信息,解答下列问题:

(1)表中a=8,b=0.3,并补全直方图
(2)若用扇形统计图描述此成绩分布情况,则分数段80≤x<100对应扇形的圆心角度数是144°;
(3)请估计该年级分数在60≤x<100的学生有多少人?
| 少分数段(x表示分数) | 频数 | 频率 |
| 50≤x<60 | 4 | 0.1 |
| 60≤x<70 | a | 0.2 |
| 70≤x<80 | 12 | b |
| 80≤x<90 | 10 | 0.25 |
| 90≤x<100 | 6 | 0.15 |

(1)表中a=8,b=0.3,并补全直方图
(2)若用扇形统计图描述此成绩分布情况,则分数段80≤x<100对应扇形的圆心角度数是144°;
(3)请估计该年级分数在60≤x<100的学生有多少人?
9.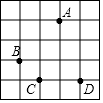 如图,每个小正方形的边长都是1,图中A,B,C,D四个点分别为小正方形的顶点,下列说法:
如图,每个小正方形的边长都是1,图中A,B,C,D四个点分别为小正方形的顶点,下列说法:
①△ACD的面积是有理数;
②四边形ABCD的四条边的长度都是无理数;
③四边形ABCD的三条边的长度是无理数,一条边的长度是有理数.
其中说法正确的有( )
 如图,每个小正方形的边长都是1,图中A,B,C,D四个点分别为小正方形的顶点,下列说法:
如图,每个小正方形的边长都是1,图中A,B,C,D四个点分别为小正方形的顶点,下列说法:①△ACD的面积是有理数;
②四边形ABCD的四条边的长度都是无理数;
③四边形ABCD的三条边的长度是无理数,一条边的长度是有理数.
其中说法正确的有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
6.在Rt△ABC 中,∠ACB=90°,若D为AB的中点,CD=6,则AB的长为( )
| A. | 24 | B. | 12 | C. | 6 | D. | 3 |
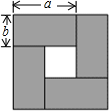 如图,是用四张相同的长方形纸片拼成的图形,其中长方形纸片的长为a,宽为b.请利用图中空白部分的面积的不同表示方法写出一个关于a,b的恒等式(a-b)2=(a+b)2-4ab.
如图,是用四张相同的长方形纸片拼成的图形,其中长方形纸片的长为a,宽为b.请利用图中空白部分的面积的不同表示方法写出一个关于a,b的恒等式(a-b)2=(a+b)2-4ab.