��Ŀ����
17��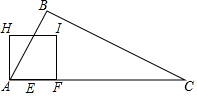 ��ͼ����Rt��ABC�У���B=90�㣬AB=$\frac{1}{2}$BC��AC=10cm������E�ӵ�A��������2cm/s���ٶ���AC���C�˶���ͬʱ����F�ӵ�A��������4cm/s���ٶ���A-C-A�˶�������E�����յ�Cʱ����F��ֹ֮ͣ�˶�������F���ڵ�E�ĶԳƵ�G�����߶�GF�Ƶ�G��ʱ����ת90��õ��߶�GH����GF��GHΪ����������FGHI�����E���˶�ʱ��Ϊts��
��ͼ����Rt��ABC�У���B=90�㣬AB=$\frac{1}{2}$BC��AC=10cm������E�ӵ�A��������2cm/s���ٶ���AC���C�˶���ͬʱ����F�ӵ�A��������4cm/s���ٶ���A-C-A�˶�������E�����յ�Cʱ����F��ֹ֮ͣ�˶�������F���ڵ�E�ĶԳƵ�G�����߶�GF�Ƶ�G��ʱ����ת90��õ��߶�GH����GF��GHΪ����������FGHI�����E���˶�ʱ��Ϊts����1���ú�t�Ĵ���ʽ��ʾ�߶�CF�ij���
��2�����E���F�غ�ʱt��ֵ��
��3����E���F�غ�֮ǰ����������FGHI��Rt��ABC�ص����ֵ�ͼ�����ı���ʱ�����ص�����ͼ�ε����S��t�ĺ�����ϵʽ��
��4��ֱ��д��ֱ��BI��AC��ֱʱt��ֵ��
���� ��1������������ֱ��ʾFC�ij����ɣ�
��2����F��C��Aʱ���Ż���E��F�غϣ�����2.5��t��5ʱ����ͼ1����E���F�غϣ�����EC=FC��ʽ������ɣ�
��3����ͼ�ο�֪������E���F�غ�֮�����ɵ�������FGHI��AC���·�����Rt��ABC���ص����֣������0��t��$\frac{10}{3}$ʱ����������FGHI��Rt��ABC�ص����ֵ�ͼ�����ı���ʱ��������������ۣ�
���ȼ��㵱I��BC��ʱt��ֵ����ͼ2����ʱt=$\frac{5}{6}$��
��0��t��$\frac{5}{6}$ʱ����ͼ4��������FGHI��Rt��ABC�ص����ֵ�ͼ�����ı���AFIG������S������AFIH-S��AGH�������S�Ĺ�ϵʽ��
�ڼ��㵱B��HI��ʱ����ͼ3����ʱt=1��
��1��t��5ʱ����ͼ5���ص����ֵ�ͼ�����ı���AFGB������S=S��ABC-S��CFG�������S�Ĺ�ϵʽ��
����ͼ6����F��C��Aʱ������GH����Bʱ������EG=FE����ʽ����t=$\frac{11}{4}$����ͼ7��H��BC��ʱ������2GH=GC������t=$\frac{25}{8}$��
��$\frac{11}{4}$��t��$\frac{25}{8}$ʱ����ͼ8���ص����ֵ��ı���ΪGFIH���������������ʽ���S�Ĺ�ϵʽ��
���ȼ��㵱I��BC��ʱ��t=$\frac{45}{14}$��
��$\frac{45}{14}$��t��$\frac{10}{3}$ʱ���ص����ֵ��ı�����������GFIH�����������ʽ���㼴�ɣ�
��4����BI��ACʱ����ͼ10����ʱBF��AC�����ù��ɶ�������AM=2$\sqrt{5}$t��֤����BMI�ס�BAF����AM=$\frac{1}{2}$AB����ʽ�����t��ֵ��
���  �⣺��1����0��t��2.5ʱ��FC=10-4t��
�⣺��1����0��t��2.5ʱ��FC=10-4t��
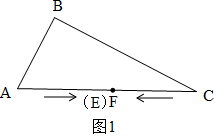
��2.5��t��5ʱ��AC+FC=4t��FC=4t-10��
��2����2.5��t��5ʱ����ͼ1����E���F�غϣ�
EC=FC��
��10-2t=4t-10��
6t=20��
t=$\frac{10}{3}$��
�𣺵�E���F�غ�ʱt��ֵ��$\frac{10}{3}$s��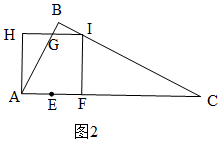
��3�������������
�ٵ�I��BC��ʱ����ͼ2��
Rt��IFC��tan��C=$\frac{FI}{FC}=\frac{1}{2}$��
��FC=2FI��
10-4t=2��4t��
t=$\frac{5}{6}$��
��Rt��ABC����AB=x����BC=2x��
�ɹ��ɶ����ã�AC=$\sqrt{5}$x=10��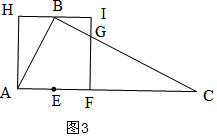
x=2$\sqrt{5}$��
��AB=2$\sqrt{5}$��BC=4$\sqrt{5}$��
��B��HI��ʱ����ͼ3��
S��ABC=$\frac{1}{2}$AB•BC=$\frac{1}{2}$AC•AH��
2$\sqrt{5}$��$4\sqrt{5}$=10AH��
AH=4��
AH=AF=4t=4��
t=1��
��0��t��$\frac{5}{6}$ʱ����ͼ4��������FGHI��Rt��ABC�ص����ֵ�ͼ�����ı���AFIG��
���ı���AFIH�������Σ�
���HAF=90�㣬AF=AH=4t��
���HAG+��GAF=90�㣬
�ߡ�B=90�㣬
���C+��GAF=90�㣬
���C=��HAG��
��AB=$\frac{1}{2}$BC��
��tan��C=tan��HAG=$\frac{AB}{BC}=\frac{1}{2}$��
��$\frac{GH}{AH}$=$\frac{1}{2}$��
��AH=2GH=4t��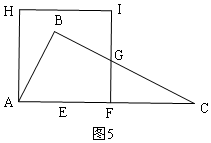
��GH=2t��
��S=S������AFIH-S��AGH=4t•4t-$\frac{1}{2}$•2t•4t=12t2��
�ڵ�1��t��5ʱ����ͼ5���ص����ֵ�ͼ�����ı���AFGB��
��FC=10-4t��
��FG=$\frac{1}{2}$FC=5-2t��
��S=S��ABC-S��CFG=$\frac{1}{2}$��$2\sqrt{5}$��$4\sqrt{5}$-$\frac{1}{2}$��5-2t����10-4t����
S=-4t2+20t-5��
����ͼ6����F��C��Aʱ����GH����B��
��Rt��ABG��cos��A=$\frac{AG}{AB}=\frac{AB}{AC}$��
��$\frac{AG}{2\sqrt{5}}=\frac{2\sqrt{5}}{10}$��
��AG=2��
��FC=4t-10��
��G��F���ڵ�E�ԳƵã�EG=FE��
AE-AG=EC-FC��
2t-2=10-2t-��4t-10����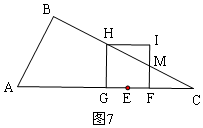
t=$\frac{11}{4}$��
��ͼ7��H��BC��ʱ��
��EF=EC-FC=10-2t-��4t-10��=20-6t��
��GH=2EF=2��20-6t��=40-12t��
tan��C=$\frac{GH}{GC}=\frac{1}{2}$��
��2GH=GC��
2��40-12t��=40-12t+4t-10��
40-12t=4t-10��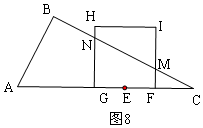
16t=50��
t=$\frac{25}{8}$��
��$\frac{11}{4}$��t��$\frac{25}{8}$ʱ����ͼ8���ص����ֵ��ı���ΪGFMN��
FM=$\frac{1}{2}$FC=2t-5��
GC=2EF+FC=40-12t+4t-10=30-8t��
GN=$\frac{1}{2}$GC=15-4t��
��S=S����GFMN=$\frac{1}{2}$��FM+GN��•GF=$\frac{1}{2}$��2t-5+15-4t����40-12t����
S=12t2-100t+300��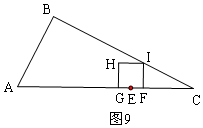
����ͼ9����I��BC��ʱ��
FI=$\frac{1}{2}$CF=2t-5��
FG=40-12t��
��FG=FI��
��40-12t=2t-5��
t=$\frac{45}{14}$��
��$\frac{45}{14}$��t��$\frac{10}{3}$ʱ���ص����ֵ��ı�����������GFIH��
S=GF2=��40-12t��2=144t2-960t+1600��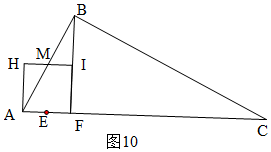
�����������ص�����ͼ�ε����S��t�ĺ�����ϵʽ��S=$\left\{\begin{array}{l}{12{t}^{2}��0��t��\frac{5}{6}��}\\{-4{t}^{2}+20t-5��1��t��5��}\\{12{t}^{2}-100t+300��\frac{11}{4}��t��\frac{25}{8}��}\\{144{t}^{2}-960t+1600��\frac{45}{14}��t��\frac{10}{3}��}\end{array}\right.$��
��4����BI��ACʱ����ͼ10����ʱBF��AC��
��Rt��AHM��AH=4t��HM=2t��
�ɹ��ɶ�������AM=$\sqrt{��4t��^{2}+��2t��^{2}}$=2$\sqrt{5}$t��
��MI=HI-HM=4t-2t=2t��
��MI��AF��
���BMI�ס�BAF��
��$\frac{BM}{AB}=\frac{MI}{AF}$=$\frac{2t}{4t}$=$\frac{1}{2}$��
��AB=2BM��
��AM=$\frac{1}{2}$AB��
2$\sqrt{5}$t=$\frac{1}{2}$��$2\sqrt{5}$��
t=$\frac{1}{2}$��
��ֱ��BI��AC��ֱʱt��ֵ��$\frac{1}{2}$��
���� �������ı��ε��ۺ��⣬�ѶȽϴ������⣬�����ǵ����ʣ��������������ε����ʡ����ɶ����������˶������⡢ͬ�ǵ����Ǻ����Լ����������Ƶ����ʺ��ж���������κ������ϣ����ݶ���ε������ʽ��Ͳ�Ĺ�ϵ�����κ����Ĺ�ϵʽ��ע����������ص��������ı���ʱ��t��ȡֵ��

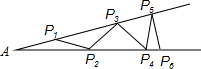 �α���Ŀ������������������һ��˼���⣬��ͼ�ּ��У���A=20�㣬���ϵȳ��ĸ������ӹ̸ּܣ���AP1=P1P2���������ĸ���������Ҫ���ٸ���
�α���Ŀ������������������һ��˼���⣬��ͼ�ּ��У���A=20�㣬���ϵȳ��ĸ������ӹ̸ּܣ���AP1=P1P2���������ĸ���������Ҫ���ٸ���
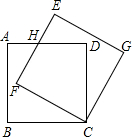 ��ͼ���߳�Ϊ10��������ABCD�Ƶ�C��˳ʱ�뷽����ת30���õ�������EFCG��EF��AD�ڵ�H����ôDH�ij�Ϊ$\frac{10\sqrt{3}}{3}$��
��ͼ���߳�Ϊ10��������ABCD�Ƶ�C��˳ʱ�뷽����ת30���õ�������EFCG��EF��AD�ڵ�H����ôDH�ij�Ϊ$\frac{10\sqrt{3}}{3}$��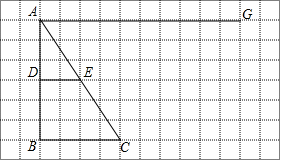 ��ͼ��������ͼ�У��С�ABC���߶�DE�����߶�AG���Ƿ���ڵ�M��ʹ�á�MEC���ADE���ƣ������ڣ�������ͼ��ȷ�������еĵ�M����ѡ������һ��˵�����ɣ��������ڣ�Ҳ��˵�����ɣ���ͼ�и�����ڸ���ϣ���
��ͼ��������ͼ�У��С�ABC���߶�DE�����߶�AG���Ƿ���ڵ�M��ʹ�á�MEC���ADE���ƣ������ڣ�������ͼ��ȷ�������еĵ�M����ѡ������һ��˵�����ɣ��������ڣ�Ҳ��˵�����ɣ���ͼ�и�����ڸ���ϣ���