题目内容
13.已知x2-2x+3y+5=0,则y-x的最大(填“大”或“小”)值为-$\frac{19}{12}$.分析 由x、y满足x2-2x+3y+5=0,可得出y=-$\frac{1}{3}$x2+$\frac{2}{3}$x-$\frac{5}{3}$,进而得出y-x=-$\frac{1}{3}$x2-$\frac{1}{3}$x-$\frac{5}{3}$,将其配方后利用偶成方的非负性即可得出y-x存在最大值,再找出最大值即可.
解答 解:∵x2-2x+3y+5=0,
∴y=-$\frac{1}{3}$x2+$\frac{2}{3}$x-$\frac{5}{3}$,
∴y-x=-$\frac{1}{3}$x2-$\frac{1}{3}$x-$\frac{5}{3}$=-$\frac{1}{3}$$(x+\frac{1}{2})^{2}$-$\frac{19}{12}$.
∵$(x+\frac{1}{2})^{2}$≥0,
∴-$\frac{1}{3}$$(x+\frac{1}{2})^{2}$≤0,
∴y-x有最大值,最大值为-$\frac{19}{12}$.
故答案为:大;-$\frac{19}{12}$.
点评 本题考查二次函数的性质、配方法的应用以及偶次方的非负性,根据x、y之间的关系找出y-x关于x的二次函数是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
18.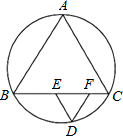 如图,$\widehat{AB}$、$\widehat{BC}$、$\widehat{CA}$度数比为12:13:11,在弧BC上取一点D,过D分别作弦AC、弦AB的平行线,交弦BC于E、F两点,则∠EDF的度数( )
如图,$\widehat{AB}$、$\widehat{BC}$、$\widehat{CA}$度数比为12:13:11,在弧BC上取一点D,过D分别作弦AC、弦AB的平行线,交弦BC于E、F两点,则∠EDF的度数( )
 如图,$\widehat{AB}$、$\widehat{BC}$、$\widehat{CA}$度数比为12:13:11,在弧BC上取一点D,过D分别作弦AC、弦AB的平行线,交弦BC于E、F两点,则∠EDF的度数( )
如图,$\widehat{AB}$、$\widehat{BC}$、$\widehat{CA}$度数比为12:13:11,在弧BC上取一点D,过D分别作弦AC、弦AB的平行线,交弦BC于E、F两点,则∠EDF的度数( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
2.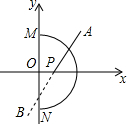 如图,在平面直角坐标系中,以原点O为圆心,3为半径的半圆,直线AB:y=x+b与x轴交于点P(x,0),若直线AB与半圆弧有公共点,则x值的范围是( )
如图,在平面直角坐标系中,以原点O为圆心,3为半径的半圆,直线AB:y=x+b与x轴交于点P(x,0),若直线AB与半圆弧有公共点,则x值的范围是( )
 如图,在平面直角坐标系中,以原点O为圆心,3为半径的半圆,直线AB:y=x+b与x轴交于点P(x,0),若直线AB与半圆弧有公共点,则x值的范围是( )
如图,在平面直角坐标系中,以原点O为圆心,3为半径的半圆,直线AB:y=x+b与x轴交于点P(x,0),若直线AB与半圆弧有公共点,则x值的范围是( )| A. | -3≤x≤3$\sqrt{2}$ | B. | -3≤x≤3 | C. | -3$\sqrt{2}$≤x≤3 | D. | 0≤x≤3$\sqrt{2}$ |
3.下列各式中,从左到右的变形是因式分解的是( )
| A. | a2c-a2b+1=a2(c-b)+1 | B. | a(x+y+1)=ax+ay+a | ||
| C. | (x+3y)(x-3y)=x2-9y2 | D. | 4x2-1=(2x+1)(2x-1) |
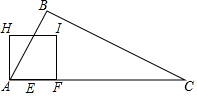 如图,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,动点E从点A出发,以2cm/s的速度沿AC向点C运动;同时动点F从点A出发,以4cm/s的速度沿A-C-A运动;当点E到达终点C时,点F随之停止运动.作点F关于点E的对称点G,将线段GF绕点G逆时针旋转90°得到线段GH,以GF,GH为边作正方形FGHI,设点E的运动时间为ts.
如图,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,动点E从点A出发,以2cm/s的速度沿AC向点C运动;同时动点F从点A出发,以4cm/s的速度沿A-C-A运动;当点E到达终点C时,点F随之停止运动.作点F关于点E的对称点G,将线段GF绕点G逆时针旋转90°得到线段GH,以GF,GH为边作正方形FGHI,设点E的运动时间为ts. 如图,在△ABC中,cosB=$\frac{\sqrt{2}}{2}$,sinC=$\frac{3}{5}$,AC=10,则△ABC的面积为42.
如图,在△ABC中,cosB=$\frac{\sqrt{2}}{2}$,sinC=$\frac{3}{5}$,AC=10,则△ABC的面积为42.