题目内容
5.计算:(1)-18+6+7-5
(2)($\frac{1}{2}$-$\frac{5}{9}$+$\frac{7}{12}$)×(-36)
(3)$\root{3}{-8}$-$\sqrt{(-1)^{2}}$+$\sqrt{9}$
(4)-12×8-8×($\frac{1}{2}$)3+4÷$\frac{1}{4}$.
分析 (1)原式结合后,相加即可得到结果;
(2)原式利用乘法分配律计算即可得到结果;
(3)原式利用立方根、平方根定义,以及二次根式性质计算即可得到结果;
(4)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
解答 解:(1)原式=-18-5+6+7=-23+13=-10;
(2)原式=-18+20-21=-19;
(3)原式=-2-1+3=0;
(4)原式=-8-1+16=7.
点评 此题考查了实数的运算,平方根、立方根定义,以及乘法运算律,熟练掌握运算法则及运算律是解本题的关键.

练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
10. 如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=4$\sqrt{2}$,CD=3$\sqrt{2}$,点P在四边形ABCD的边上.若点P到BD的距离为3,则点P的个数为( )
如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=4$\sqrt{2}$,CD=3$\sqrt{2}$,点P在四边形ABCD的边上.若点P到BD的距离为3,则点P的个数为( )
 如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=4$\sqrt{2}$,CD=3$\sqrt{2}$,点P在四边形ABCD的边上.若点P到BD的距离为3,则点P的个数为( )
如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=4$\sqrt{2}$,CD=3$\sqrt{2}$,点P在四边形ABCD的边上.若点P到BD的距离为3,则点P的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
2.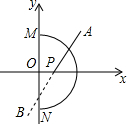 如图,在平面直角坐标系中,以原点O为圆心,3为半径的半圆,直线AB:y=x+b与x轴交于点P(x,0),若直线AB与半圆弧有公共点,则x值的范围是( )
如图,在平面直角坐标系中,以原点O为圆心,3为半径的半圆,直线AB:y=x+b与x轴交于点P(x,0),若直线AB与半圆弧有公共点,则x值的范围是( )
 如图,在平面直角坐标系中,以原点O为圆心,3为半径的半圆,直线AB:y=x+b与x轴交于点P(x,0),若直线AB与半圆弧有公共点,则x值的范围是( )
如图,在平面直角坐标系中,以原点O为圆心,3为半径的半圆,直线AB:y=x+b与x轴交于点P(x,0),若直线AB与半圆弧有公共点,则x值的范围是( )| A. | -3≤x≤3$\sqrt{2}$ | B. | -3≤x≤3 | C. | -3$\sqrt{2}$≤x≤3 | D. | 0≤x≤3$\sqrt{2}$ |
 已知:如图三角形中,请完成下列操作:
已知:如图三角形中,请完成下列操作: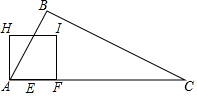 如图,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,动点E从点A出发,以2cm/s的速度沿AC向点C运动;同时动点F从点A出发,以4cm/s的速度沿A-C-A运动;当点E到达终点C时,点F随之停止运动.作点F关于点E的对称点G,将线段GF绕点G逆时针旋转90°得到线段GH,以GF,GH为边作正方形FGHI,设点E的运动时间为ts.
如图,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,动点E从点A出发,以2cm/s的速度沿AC向点C运动;同时动点F从点A出发,以4cm/s的速度沿A-C-A运动;当点E到达终点C时,点F随之停止运动.作点F关于点E的对称点G,将线段GF绕点G逆时针旋转90°得到线段GH,以GF,GH为边作正方形FGHI,设点E的运动时间为ts.