题目内容
2.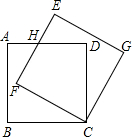 如图,边长为10的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为$\frac{10\sqrt{3}}{3}$.
如图,边长为10的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长为$\frac{10\sqrt{3}}{3}$.
分析 过点F作FI⊥BC于点BC,延长线AD交AD于J,根据题意可求出FI、FJ和JH的长度,从而求出HD的长度.
解答 解: 过点F作FI⊥BC于点BC,延长线AD交AD于J,
过点F作FI⊥BC于点BC,延长线AD交AD于J,
由题意可知:CF=BC=10,∠FCB=30°,
∴FI=5,CI=5$\sqrt{3}$
∵JI=CD=10,
∴JF=JI-FI=5,
∵∠HFC=90°,
∴∠JFH+∠IFC=∠IFC+∠FCB=90°,
∴∠JFH=∠FCB=30°,
设JH=x,则HF=2x,
∴由勾股定理可知:(2x)2=x2+52,
∴x=$\frac{5\sqrt{3}}{3}$,
∴DH=DJ-JH=$\frac{10\sqrt{3}}{3}$
故答案为:$\frac{10\sqrt{3}}{3}$.
点评 本题考查正方形的性质,涉及正方形的性质,勾股定理,旋转的性质,含30°的直角三角形的性质,本题属于中等题型.

练习册系列答案
相关题目
12.长方形的一边长等于4m+n,另一边比它小m-n,那么这个长方形的周长是( )
| A. | 7m+3n | B. | 8m+2n | C. | 14m+6n | D. | 12m+8n |
10. 如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=4$\sqrt{2}$,CD=3$\sqrt{2}$,点P在四边形ABCD的边上.若点P到BD的距离为3,则点P的个数为( )
如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=4$\sqrt{2}$,CD=3$\sqrt{2}$,点P在四边形ABCD的边上.若点P到BD的距离为3,则点P的个数为( )
 如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=4$\sqrt{2}$,CD=3$\sqrt{2}$,点P在四边形ABCD的边上.若点P到BD的距离为3,则点P的个数为( )
如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=4$\sqrt{2}$,CD=3$\sqrt{2}$,点P在四边形ABCD的边上.若点P到BD的距离为3,则点P的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
 已知:如图三角形中,请完成下列操作:
已知:如图三角形中,请完成下列操作: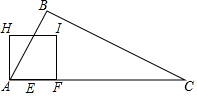 如图,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,动点E从点A出发,以2cm/s的速度沿AC向点C运动;同时动点F从点A出发,以4cm/s的速度沿A-C-A运动;当点E到达终点C时,点F随之停止运动.作点F关于点E的对称点G,将线段GF绕点G逆时针旋转90°得到线段GH,以GF,GH为边作正方形FGHI,设点E的运动时间为ts.
如图,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,动点E从点A出发,以2cm/s的速度沿AC向点C运动;同时动点F从点A出发,以4cm/s的速度沿A-C-A运动;当点E到达终点C时,点F随之停止运动.作点F关于点E的对称点G,将线段GF绕点G逆时针旋转90°得到线段GH,以GF,GH为边作正方形FGHI,设点E的运动时间为ts.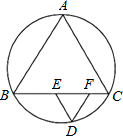 如图,$\widehat{AB}$、$\widehat{BC}$、$\widehat{CA}$度数比为12:13:11,在弧BC上取一点D,过D分别作弦AC、弦AB的平行线,交弦BC于E、F两点,则∠EDF的度数( )
如图,$\widehat{AB}$、$\widehat{BC}$、$\widehat{CA}$度数比为12:13:11,在弧BC上取一点D,过D分别作弦AC、弦AB的平行线,交弦BC于E、F两点,则∠EDF的度数( )