题目内容
7.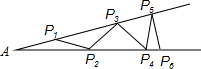 课本“目标与评定”中有这样一道思考题,如图钢架中,∠A=20°,焊上等长的钢条来加固钢架,若AP1=P1P2,问这样的钢条至多需要多少根?
课本“目标与评定”中有这样一道思考题,如图钢架中,∠A=20°,焊上等长的钢条来加固钢架,若AP1=P1P2,问这样的钢条至多需要多少根?(1)请补充完整如下解答:
解:由题意可知,P1P2=P2P3=P3P4=P4P5=…
∵∠A=20°,AP1=P1P2,
∴∠AP2P1=∠A.
∴∠P2P1P3=∠P1P3P2=40°,
同理可得,∠P3P2P4=∠P2P4P3=60°,
∠P4P3P5=∠P4P5P3=80°.
∴∠P5P4B=100°>90°,
∴对于直线P4B上任意一点P6(点P4除外),P4P5<P5P6,
∴这样的钢条至多需要4根.
(2)继续探究:当∠A=15°时,这样的钢条至多需要多少根?
分析 (1)由于焊上的钢条长度相等,并且AP1=P1P2,所以∠A=∠P1P2A,则可算出∠P2P1P3的度数,并且和∠P1P3P2度数相等,根据平角的度数为180度和三角形内角和为180度,结合等腰三角形底角度数小于90度即可求出最多能焊上的钢条数;
(2)由于焊上的钢条长度相等,并且A P1=P1P2,所以∠A=∠P1P2A,则可算出∠P2P1P3的度数,并且和∠P1P3P2度数相等,根据平角的度数为180度和三角形内角和为180度,结合等腰三角形底角度数小于90度即可求出最多能焊上的钢条数.
解答  解:(1)由题意可知,P1P2=P2P3=P3P4=P4P5=…
解:(1)由题意可知,P1P2=P2P3=P3P4=P4P5=…
∵∠A=20°,AP1=P1P2,
∴∠AP2P1=∠A.
∴∠P2P1P3=∠P1P3P2=40°,
同理可得,∠P3P2P4=∠P2P4P3=60°,
∠P4P3P5=∠P4P5P3=80°.
∴∠P5P4B=100°>90°,
∴对于直线P4B上任意一点P6(点P4除外),P4P5<P5P6,
∴这样的钢条至多需要4根;
故答案为:∠A,80°,4;
(2)如图:
∵∠A=∠P1P2A=15°,
∴∠P2P1P3=30°,∠P1P3P2=30°,
∴∠P1P2P3=120°,
∴∠P3P2P4=45°,
∴∠P3P2P4=45°,
∴∠P2P3P4=90°,
∴∠P4P3P5=60°,
∴∠P3P5P4=60°,
∴∠P3P4P5=60°,
∴∠P5P4P6=75°,
∴∠P4P6P5=75°,
∴∠P4P5P6=30°,
∴∠P6P5P7=90°,此时就不能在往上焊接了,综上所述总共可焊上5条.
点评 此题考查了三角形的内角和是180度的性质和等腰三角形的性质及三角形外角的性质;发现并利用规律是正确解答本题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
17.在平面直角坐标系中,把点P(-5,3)向右平移8个单位得到点P1,再将点P1绕原点顺时针旋转90°得到点P2,则点P2的坐标是( )
| A. | (3,3)或(-3,-3) | B. | (-3,3) | C. | (3,-3) | D. | (3,-3)或(-3,3) |
2. 如图,直线y1=kx+b过点A(0,3),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是( )
如图,直线y1=kx+b过点A(0,3),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是( )
 如图,直线y1=kx+b过点A(0,3),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是( )
如图,直线y1=kx+b过点A(0,3),且与直线y2=mx交于点P(1,m),则不等式组mx>kx+b>mx-2的解集是( )| A. | x>1 | B. | 1<x<$\frac{5}{3}$ | C. | 1<x<2 | D. | 1<x<3 |
12.长方形的一边长等于4m+n,另一边比它小m-n,那么这个长方形的周长是( )
| A. | 7m+3n | B. | 8m+2n | C. | 14m+6n | D. | 12m+8n |




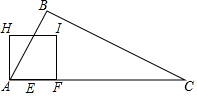 如图,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,动点E从点A出发,以2cm/s的速度沿AC向点C运动;同时动点F从点A出发,以4cm/s的速度沿A-C-A运动;当点E到达终点C时,点F随之停止运动.作点F关于点E的对称点G,将线段GF绕点G逆时针旋转90°得到线段GH,以GF,GH为边作正方形FGHI,设点E的运动时间为ts.
如图,在Rt△ABC中,∠B=90°,AB=$\frac{1}{2}$BC,AC=10cm,动点E从点A出发,以2cm/s的速度沿AC向点C运动;同时动点F从点A出发,以4cm/s的速度沿A-C-A运动;当点E到达终点C时,点F随之停止运动.作点F关于点E的对称点G,将线段GF绕点G逆时针旋转90°得到线段GH,以GF,GH为边作正方形FGHI,设点E的运动时间为ts.