题目内容
10.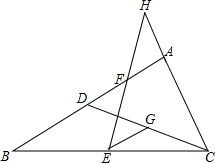 已知,如图,在△ABC中,点D在AB上,BD=AC,E,F,G分别是BC,AD,CD的中点,EF,CA的延长线相交于点H.求证:
已知,如图,在△ABC中,点D在AB上,BD=AC,E,F,G分别是BC,AD,CD的中点,EF,CA的延长线相交于点H.求证:(1)∠CGE=∠ACD+∠CAD;
(2)AH=AF.
分析 (1)由题目的已知条件可得EG是△BDC的中位线,所以EG∥BD,由此可得∠CGE=∠BDC,再根据三角形外角和定理即可证明∠CGE=∠ACD+∠CAD;
(2)连接FG,易证△FGE是等腰三角形,所以∠GFE=∠GEF,再根据平行线的性质以及对顶角相等可证明∠H=∠AFE,进而可得:AH=AF,
解答 证明(1)∵E,G分别是BC,CD的中点,
∴EG是△BDC的中位线,
∴EG∥BD,
∴∠CGE=∠BDC,
∵∠BDC=∠ACD+∠CAD,
∴∠CGE=∠ACD+∠CAD;
(2)连接FG,
∵E,F,G分别是BC,AD,CD的中点,
∴EG=$\frac{1}{2}$BD,FG=$\frac{1}{2}$AC,
∵BD=AC,
∴GE=GF,
∴∠GFE=∠GEF,
∵FG∥HC,
∴∠GFE=∠H,
∵∠GEF=∠BFE=∠AFH,
∴∠H=∠AFE,
∴AH=AF.
点评 本题考查了三角形的中位线定理,中位线是三角形中的一条重要线段,由于它的性质与线段的中点及平行线紧密相连,因此,它在几何图形的计算及证明中有着广泛的应用.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
5.下列运算中错误的是( )
| A. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | B. | $\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$ | C. | 2$\sqrt{2}$+3$\sqrt{3}$=5$\sqrt{5}$ | D. | $\sqrt{(-4)^{2}}$=4 |
19.已知AD是△ABC的中线,且△ABD比△ACD的周长大3cm,则AB与AC的差为( )
| A. | 2cm | B. | 3cm | C. | 4cm | D. | 6cm |
20.若代数式$\frac{2}{x-2}$和$\frac{3}{2x+1}$的值相等,则x的值为( )
| A. | 3 | B. | 7 | C. | -4 | D. | -8 |