题目内容
15.计算:$\frac{1}{2}$×($\sqrt{3}$-1)2+$\frac{1}{\sqrt{2}-1}$+$\sqrt{3}$-$\sqrt{\frac{12}{6}}$.分析 先利用完全平方公式计算,再进行分母有理化则可得到原式=$\frac{1}{2}$×(3-2$\sqrt{3}$+1)+$\sqrt{2}$+1+$\sqrt{3}$-$\sqrt{2}$,然后进行乘法运算后合并即可.
解答 解:原式=$\frac{1}{2}$×(3-2$\sqrt{3}$+1)+$\sqrt{2}$+1+$\sqrt{3}$-$\sqrt{2}$
=2-$\sqrt{3}$+$\sqrt{2}$+1+$\sqrt{3}$-$\sqrt{2}$
=3.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
20.在平面直角坐标系中,如果点P(a,2)在第二象限,那么点Q(-3,a)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7. 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 3 |
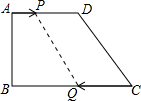 如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1cm/s的速度运动,点Q从C点开始沿CB边向B以2cm/s的速度运动,如果P、Q分别从A、C同时出发,设运动时间为t秒.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AD=18cm,BC=21cm,点P从点A开始沿AD边向D以1cm/s的速度运动,点Q从C点开始沿CB边向B以2cm/s的速度运动,如果P、Q分别从A、C同时出发,设运动时间为t秒.
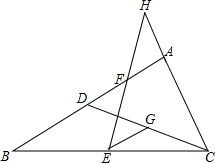 已知,如图,在△ABC中,点D在AB上,BD=AC,E,F,G分别是BC,AD,CD的中点,EF,CA的延长线相交于点H.求证:
已知,如图,在△ABC中,点D在AB上,BD=AC,E,F,G分别是BC,AD,CD的中点,EF,CA的延长线相交于点H.求证: