题目内容
19.已知AD是△ABC的中线,且△ABD比△ACD的周长大3cm,则AB与AC的差为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 6cm |
分析 根据三角形中线的定义可得BD=CD,然后根据三角形的周长公式列式计算即可得解.
解答  解:∵AD是△ABC的中线,
解:∵AD是△ABC的中线,
∴BD=DC,
∴△ABD与△ACD的周长之差=(AB+AD+BD)-(AC+AD+CD)=AB-AC,
∵△ABD比△ACD的周长大3cm,
∴AB与AC的差为3cm.
故选B.
点评 本题考查了三角形的角平分线、中线和高线,熟记概念并求出两三角形周长的差等于AB-AC是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
7. 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 3 |
14.若关于x,y的二元一次方程组$\left\{\begin{array}{l}{x+y=k}\\{2x-y=8k}\end{array}\right.$的解也是二元一次方程3x+2y=10的解,则k的值为( )
| A. | 1 | B. | -2 | C. | 2 | D. | 4 |
11.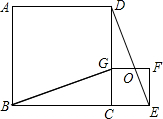 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,GD=2CG,连接BG、DE,DE和FG相交于点O.下列结论:
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,GD=2CG,连接BG、DE,DE和FG相交于点O.下列结论:
①△BCG≌△DCE;②BG⊥DE;③$\frac{DG}{GC}$=$\frac{CO}{CE}$;④4S△EFO=S△DGO.
其中正确的结论有( )
 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,GD=2CG,连接BG、DE,DE和FG相交于点O.下列结论:
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,GD=2CG,连接BG、DE,DE和FG相交于点O.下列结论:①△BCG≌△DCE;②BG⊥DE;③$\frac{DG}{GC}$=$\frac{CO}{CE}$;④4S△EFO=S△DGO.
其中正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9.在△ABC中,已知∠A=∠B=45°,BC=$\sqrt{2}$,则边AB的长为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
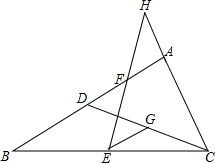 已知,如图,在△ABC中,点D在AB上,BD=AC,E,F,G分别是BC,AD,CD的中点,EF,CA的延长线相交于点H.求证:
已知,如图,在△ABC中,点D在AB上,BD=AC,E,F,G分别是BC,AD,CD的中点,EF,CA的延长线相交于点H.求证: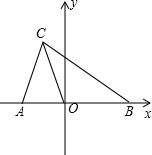 如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,3),且|$\frac{a}{2}$$+\frac{b}{3}$|+(4a-b+11)2=0.
如图,在平面直角坐标系中,A(a,0),B(b,0),C(-1,3),且|$\frac{a}{2}$$+\frac{b}{3}$|+(4a-b+11)2=0.