题目内容
2.观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187…,则32015的末尾数字是( )| A. | 9 | B. | 1 | C. | 3 | D. | 7 |
分析 由上述的几个例子可以看出个位数字的变化,1次方为3,2次方为9,3次方为7,4次方为1,5次方为3,即个位的数字是以4为周期的变化的,故2015除以4余3,即个位数为7.
解答 解:通过观察31=3,32=9,33=27,34=81,35=243,36=729上述的几个式子,
易知1次方为末位数字是3,2次方末位数字是为9,3次方末位数字是为7,4次方末位数字是为1,
5次方末位数字是为3,个位数字的变化是以3,9,7,1为周期,即周期为4,
又因为2015÷4=503…3,故32015的末尾数字与33的尾数相同为7.
故选:D.
点评 本题主要考查尾数特征,根据已知数据的尾数变化规律是解题关键.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
7. 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
 如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )
如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 3 |
14.若关于x,y的二元一次方程组$\left\{\begin{array}{l}{x+y=k}\\{2x-y=8k}\end{array}\right.$的解也是二元一次方程3x+2y=10的解,则k的值为( )
| A. | 1 | B. | -2 | C. | 2 | D. | 4 |
11.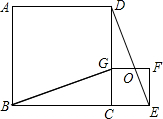 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,GD=2CG,连接BG、DE,DE和FG相交于点O.下列结论:
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,GD=2CG,连接BG、DE,DE和FG相交于点O.下列结论:
①△BCG≌△DCE;②BG⊥DE;③$\frac{DG}{GC}$=$\frac{CO}{CE}$;④4S△EFO=S△DGO.
其中正确的结论有( )
 如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,GD=2CG,连接BG、DE,DE和FG相交于点O.下列结论:
如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,GD=2CG,连接BG、DE,DE和FG相交于点O.下列结论:①△BCG≌△DCE;②BG⊥DE;③$\frac{DG}{GC}$=$\frac{CO}{CE}$;④4S△EFO=S△DGO.
其中正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.下列运算中,正确的是( )
| A. | $\sqrt{-2}$×$\sqrt{-3}$=$\sqrt{(-2)×(-3)}$=$\sqrt{6}$ | B. | 2$\sqrt{3}$×3$\sqrt{2}$=6$\sqrt{6}$ | C. | $\sqrt{{a}^{2}-4}$=$\sqrt{{a}^{2}}$-$\sqrt{4}$=a-2 | D. | 3$\sqrt{2}$+2$\sqrt{3}$=5$\sqrt{5}$ |
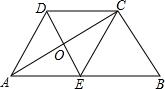 如图,在Rt△ABC中,CE是斜边AB上的中线,CD∥AB,且CD=CE,求证:
如图,在Rt△ABC中,CE是斜边AB上的中线,CD∥AB,且CD=CE,求证:
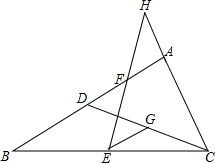 已知,如图,在△ABC中,点D在AB上,BD=AC,E,F,G分别是BC,AD,CD的中点,EF,CA的延长线相交于点H.求证:
已知,如图,在△ABC中,点D在AB上,BD=AC,E,F,G分别是BC,AD,CD的中点,EF,CA的延长线相交于点H.求证: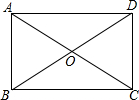 如图,在矩形ABCD中,两条对角线AC、BD相交于点O,AB=OA=4cm,求BD与AD的长.
如图,在矩形ABCD中,两条对角线AC、BD相交于点O,AB=OA=4cm,求BD与AD的长.