题目内容
7.(1)$\sqrt{12}$-3tan30°+(4-π)0-($\frac{1}{2}$)-1(2)先化简,再求值:($\frac{3}{x+1}$-x+1)÷$\frac{{x}^{2}+4x+4}{x+1}$,其中x=$\sqrt{2}$-2.
分析 (1)根据特殊角的三角函数值以及零指数幂,负整数指数幂的意义即可求出答案.
解答 解:(1)原式=2$\sqrt{3}$-3×$\frac{\sqrt{3}}{3}$+1-2
=$\sqrt{3}$-1
(2)当x=$\sqrt{2}-2$
∴原式=($\frac{3}{x+1}$-x+1)×$\frac{x+1}{(x+2)^{2}}$
=$\frac{2-x}{x+2}$
=2$\sqrt{2}$-1
点评 本题考查学生的计算能力,解题的关键是熟练运用运算法则,本题属于基础题型.

练习册系列答案
相关题目
17. 已知一次函数y=(a+1)x+b的图象如图所示,那么a的取值范围是( )
已知一次函数y=(a+1)x+b的图象如图所示,那么a的取值范围是( )
 已知一次函数y=(a+1)x+b的图象如图所示,那么a的取值范围是( )
已知一次函数y=(a+1)x+b的图象如图所示,那么a的取值范围是( )| A. | a<-1 | B. | a>-1 | C. | a≤-1 | D. | a≥-1 |

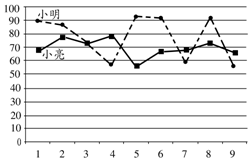 小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )
小明和小亮组成团队参加某科学比赛.该比赛的规则是:每轮比赛一名选手参加,若第一轮比赛得分满60则另一名选手晋级第二轮,第二轮比赛得分最高的选手所在团队取得胜利.为了在比赛中取得更好的成绩,两人在赛前分别作了九次测试,如图为二人测试成绩折线统计图,下列说法合理的是( )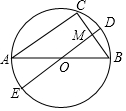 如图,AB是⊙O的直径,AC.BC是⊙O的弦,直径DE⊥BC于点M.若点E在优弧$\widehat{CAB}$上,AC=8,BC=6,则EM=9.
如图,AB是⊙O的直径,AC.BC是⊙O的弦,直径DE⊥BC于点M.若点E在优弧$\widehat{CAB}$上,AC=8,BC=6,则EM=9.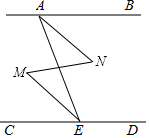 如图,∠BAE+∠AED=180°,∠M=∠N.求证:∠BAN=∠CEM.
如图,∠BAE+∠AED=180°,∠M=∠N.求证:∠BAN=∠CEM.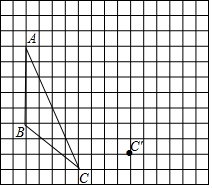 画图并填空,如图:方格纸中每个小正方形的边长都为1,在方格纸中将△ABC经过一次平移后得到△A′B′C′.图中标出了点C的对应点C′.
画图并填空,如图:方格纸中每个小正方形的边长都为1,在方格纸中将△ABC经过一次平移后得到△A′B′C′.图中标出了点C的对应点C′.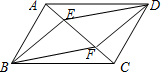 如图,已知?ABCD,BE⊥AC于点E,DF⊥AC于点F,连接DE、BF,求证:DE=BF.
如图,已知?ABCD,BE⊥AC于点E,DF⊥AC于点F,连接DE、BF,求证:DE=BF.