题目内容
12.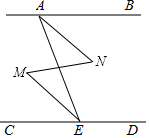 如图,∠BAE+∠AED=180°,∠M=∠N.求证:∠BAN=∠CEM.
如图,∠BAE+∠AED=180°,∠M=∠N.求证:∠BAN=∠CEM.证明:∵∠BAE+∠AED=180°,(已知)
∴AB∥CD,(同旁内角互补,两直线平行)
∴∠BAE=∠CEA.(两直线平行,内错角相等)
又∵∠M=∠N (已知)
∴AN∥ME(内错角相等,两直线平行)
∴∠BAE=∠MEA.(两直线平行,内错角相等)
∴∠BAE-∠MAE=∠CEA-∠MEA.(等式性质1)
即:∠BAN=∠CEM.(等量代换)
分析 由平行线的判定与性质即可得出结论.
解答 解:∵∠BAE+∠AED=180°,(已知)
∴AB∥CD,(同旁内角互补,两直线平行)
∴∠BAE=∠CEA.(两直线平行,内错角相等)
又∵∠M=∠N (已知)
∴AN∥ME(内错角相等,两直线平行)
∴∠BAE=∠MEA.(两直线平行,内错角相等)
∴∠BAE-∠MAE=∠CEA-∠MEA.(等式性质1)
即:∠BAN=∠CEM.(等量代换)
故答案为:同旁内角互补,两直线平行;∠BAE;∠CEA; AN,ME;内错角相等,两直线平行; 两直线平行,内错角相等.
点评 本题考查了平行线的判定与性质;熟练掌握平行线的判定与性质是解决问题的关键.

练习册系列答案
相关题目
2.在平面直角坐标系中,已知点A(-1,0),B(1,2),将线段AB平移后得线段CD,若点A的对应点C的坐标为(1,-2),则点B的对应点D的坐标为( )
| A. | (3,0) | B. | (3,-1) | C. | (3,-3) | D. | (-1,3) |
20.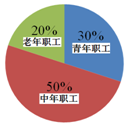 某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.
某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.
为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
表2:小王抽样调查单位10名职工的健康指数
表3:小李抽样调查单位10名职工的健康指数
根据上述材料回答问题:
小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
 某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.
某单位有职工200人,其中青年职工(20-35岁),中年职工(35-50岁),老年职工(50岁及以上)所占比例如扇形统计图所示.为了解该单位职工的健康情况,小张、小王和小李各自对单位职工进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1:小张抽样调查单位3名职工的健康指数
| 年龄 | 26 | 42 | 57 |
| 健康指数 | 97 | 79 | 72 |
| 年龄 | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
| 健康指数 | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
| 年龄 | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
| 健康指数 | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
小张、小王和小李三人中,谁的抽样调查的数据能够较好地反映出该单位职工健康情况,并简要说明其他两位同学抽样调查的不足之处.
1.“3.15“植树节活动后,某校对栽下的甲、乙、丙、丁四个品种的树苗进行成活率观测,以下是根据观测数据制成的统计图表的一部分;
表1:栽下的各品种树苗棵数统计表表
请你根据以上信息解答下列问题:
(1)这次栽下的四个品种的树苗共500棵,乙品种树苗100棵.
(2)图1中,甲30%、乙20%;
(3)已知这批树苗成活率为90%,将图2补充完整.
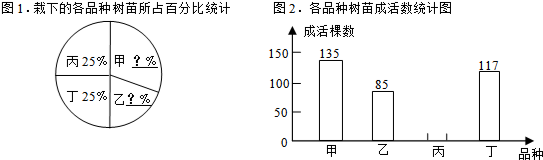
表1:栽下的各品种树苗棵数统计表表
| 植树品种 | 甲种 | 乙种 | 丙种 | 丁种 |
| 植树棵数 | 150 | 125 | 125 |
(1)这次栽下的四个品种的树苗共500棵,乙品种树苗100棵.
(2)图1中,甲30%、乙20%;
(3)已知这批树苗成活率为90%,将图2补充完整.

2.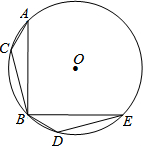 如图,△ABC是⊙O的内接三角形,∠A=30°,BC=$\sqrt{2}$,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为( )
如图,△ABC是⊙O的内接三角形,∠A=30°,BC=$\sqrt{2}$,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为( )
 如图,△ABC是⊙O的内接三角形,∠A=30°,BC=$\sqrt{2}$,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为( )
如图,△ABC是⊙O的内接三角形,∠A=30°,BC=$\sqrt{2}$,把△ABC绕点O按逆时针方向旋转90°得到△BED,则对应点C、D之间的距离为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |