Question

2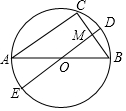．如图，AB是⊙O的直径，AC．BC是⊙O的弦，直径DE⊥BC于点M．若点E在优弧$\widehat{CAB}$上，AC=8，BC=6，则EM=9．

Answer 1

分析 根据垂径定理得到CM=BM，根据相似三角形的性质得到OM=4，根据勾股定理得到AB=10，于是得到结论．

解答 解：∵直径DE⊥BC于点M．
∴CM=BM，
∵AO=OB，
∴OM∥AC，
∴△BOM∽△BAC，
∴$\frac{OM}{AC}=\frac{OB}{AB}=\frac{1}{2}$，
∴OM=4，
∵AB是⊙O的直径，
∴∠C=90°，
∴AB=10，
∴OE=5，
∴EM=9，
故答案为：9．

点评 本题主要考查了圆周角定理，平行线的判定，相似三角形的判定和性质，熟练掌握圆周角定理是解决问题的关键．