题目内容
17．解不等式（组），并把解集表示在数轴上（1）2x-1＞$\frac{3x-1}{2}$
（2）$\left\{\begin{array}{l}{2x+5≤3（x+2）}\\{\frac{1-2x}{3}+\frac{1}{5}＞0}\end{array}\right.$．
分析 （1）先去分母，再移项，合并同类项，将不等式解集表示在数轴上即可；
（2）分别求出各不等式的解集，再求出其公共解集，并在数轴上表示出来即可．
解答 解：（1）去分母，得：4x-2＞3x-1，
移项，得：4x-3x＞2-1，
合并同类项，得：x＞1，
将不等式解集表示在数轴上如图：
；
（2）∵由①得：x≥-1，
由②得：x＜$\frac{4}{5}$，
∴不等式组的解集为-1≤x＜$\frac{4}{5}$，
表示在数轴上，如图所示：
．
点评 本题考查的是解一元一次不等式组，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
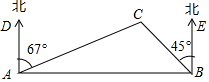一艘救生船在码头A接到小岛C处一艘渔船的求救信号，立即出发，沿北偏东67°方向航行10海里到达小岛C处，将人员撤离到码头A张东方向的码头B，测得小岛C位于码头B西北方向，求码头B与小岛C的距离（结果精确到0.1海里）．
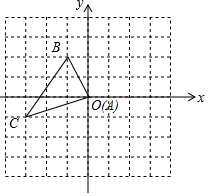在边长为1的正方形网格中建立平面直角坐标系，△ABC位置如图．
2．在平面直角坐标系中，已知点A（-1，0），B（1，2），将线段AB平移后得线段CD，若点A的对应点C的坐标为（1，-2），则点B的对应点D的坐标为（ ）
| A． | （3，0） | B． | （3，-1） | C． | （3，-3） | D． | （-1，3） |
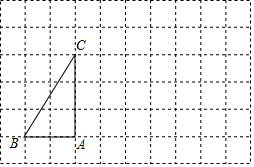已知，△ABC在方格纸（每个小方格的边长为1个单位长度）中的位置如图，将△ABC绕点A旋转90°，再向右平移3个单位长度得△DEF，请在方格纸中画出△DEF．
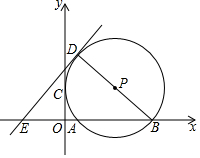如图，已知⊙P与x轴交于A和B（9，0）两点，与y轴的正半轴相切与点C（0，3），作⊙P的直径BD，过点D作直线DE⊥BD，交x轴于E点，若点P在双曲线y=$\frac{15}{x}$上，则直线DE的解析式为y=$\frac{12}{7}$x+$\frac{30}{7}$．