题目内容
18.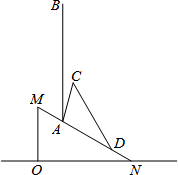 今年夏天我市出现厄尔尼诺现象极端天气,多地引发滑坡、山洪等严重自然灾害.如图所示,ON为水平线,斜坡MN的坡比为1:$\sqrt{3}$,斜坡上一棵大树树干AB(树干AB垂直于底面ON)被大风刮倾斜15°后折断倒在山坡上,树的顶部恰好接触到坡面,经测量,大树被折断部分与坡面所成的角∠ADC=30°,AD=8米,∠BAC=15°.
今年夏天我市出现厄尔尼诺现象极端天气,多地引发滑坡、山洪等严重自然灾害.如图所示,ON为水平线,斜坡MN的坡比为1:$\sqrt{3}$,斜坡上一棵大树树干AB(树干AB垂直于底面ON)被大风刮倾斜15°后折断倒在山坡上,树的顶部恰好接触到坡面,经测量,大树被折断部分与坡面所成的角∠ADC=30°,AD=8米,∠BAC=15°.(1)求这棵大树原来的高度;(参考数据:$\sqrt{2}≈1.414,\sqrt{3}$≈1.732.结果精确到0.1米)
(2)某高速路段由于滑坡,需要在一定时间内进行抢修,若甲队单独做正好按时完成,而乙队由于人少,单独做则超期3个小时才能完成.现甲乙两队合作2小时后,甲队又有新任务,余下的由乙队单独做,正好按期完成.求乙队单独完成全部工程需多少小时?
分析 (1)过点A作AH⊥CD,垂足为H,解Rt△ADH中,求得AH,DH,在RT△ACH中,求得CH=AH=4米,然后根据AB=AC+CD即可求解;
(2)设乙队单独完成需要x小时,则甲队单独完成需要(x-3)小时,根据甲乙两队合作2小时后,甲队又有新任务,余下的由乙队单独做,正好按期完成建立方程,求解即可.
解答  解:(1)过点A作AH⊥CD,垂足为H,
解:(1)过点A作AH⊥CD,垂足为H,
∵在Rt△ADH中,∠ADH=30°,AD=8米,
∴AH=$\frac{1}{2}$AD=4米,DH=$\sqrt{3}$AH=4$\sqrt{3}$米.
∵斜坡MN的坡比为1:$\sqrt{3}$,
∴tan∠MNO=1:$\sqrt{3}$=$\frac{\sqrt{3}}{3}$,
∴∠MNO=30°,
∴∠M=60°=∠BAM,
∵∠BAC=15°,
∴∠CAD=180°-∠BAM-∠BAC=180°-60°-15°=105°,
∴∠C=180°-∠CAD-∠ADC=180°-105°-30°=45°.
∵在Rt△ACH中,∠C=45°,
∴CH=AH=4米,AC=$\sqrt{2}$AH=4$\sqrt{2}$米.
∴AB=AC+CD=4$\sqrt{2}$+4+4$\sqrt{3}$≈16.6(米).
答:这棵大树原来的高度约16.6米;
(2)设乙队单独完成需要x小时,则甲队单独完成需要(x-3)小时,
根据题意得($\frac{1}{x}$+$\frac{1}{x-3}$)×2+$\frac{1}{x}$×(x-3-2)=1,
解得x=9.
经检验,x=9是原方程的解,也符合题意.
答:乙队单独完成全部工程需9小时.
点评 本题考查了解直角三角形的应用-坡度坡角问题,含30°角的直角三角形的性质,等腰直角三角形的性质,平行线的性质,三角形内角和定理,本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中,使问题解决.也考查了分式方程的应用.

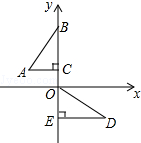 如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,2),AC=4,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,2),AC=4,则这种变换可以是( )| A. | △ABC绕点C逆时针旋转90°,再向下平移2 | |
| B. | △ABC绕点C顺时针旋转90°,再向下平移2 | |
| C. | △ABC绕点C顺时针旋转90°,再向下平移6 | |
| D. | △ABC绕点C逆时针旋转90°,再向下平移6 |
| A. | m不为0 | B. | m=2 | C. | m=-2 | D. | m=2或-2 |
 如图,在Rt△ABC中,∠ABC=90°,AB=BC=12cm,点D从点A出发沿AB以2cm/s的速度向B移动,移动过程中始终保持DE∥BC,DF∥AC(点E、F分别在AC、BC上)设运动时间为t s.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=12cm,点D从点A出发沿AB以2cm/s的速度向B移动,移动过程中始终保持DE∥BC,DF∥AC(点E、F分别在AC、BC上)设运动时间为t s. 如图:
如图: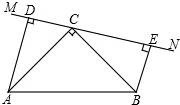 在△ABC中,∠ACB=90°,AC=BC,AD=8cm,BE=6cm,直线MN经过点C,且
在△ABC中,∠ACB=90°,AC=BC,AD=8cm,BE=6cm,直线MN经过点C,且