题目内容
6. 如图,在Rt△ABC中,∠ABC=90°,AB=BC=12cm,点D从点A出发沿AB以2cm/s的速度向B移动,移动过程中始终保持DE∥BC,DF∥AC(点E、F分别在AC、BC上)设运动时间为t s.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=12cm,点D从点A出发沿AB以2cm/s的速度向B移动,移动过程中始终保持DE∥BC,DF∥AC(点E、F分别在AC、BC上)设运动时间为t s.(1)点D出发几秒后四边形DFCE的面积为20cm2;
(2)以E为圆心,ED为半径作圆,当⊙E恰好经过点F时,求t的值.
分析 (1)根据四边形DFCE的面积=△ABC的面积-△ADE的面积-△DBF的面积=20cm2,列方程求解即可;
(2)根据题意可知DE=EF,然后列方程求解即可.
解答 解:(1)设运动时间为ts,则AD=2tcm,DB=(12-2t)cm.
根据题意得:$\frac{1}{2}×12×12$-$\frac{1}{2}×2t×2t$-$\frac{1}{2}×(12-2t)×(12-2t)$=20.
解得:t1=1,t2=5.
答:点D出发1秒或5秒后四边形DFCE的面积为20cm2.
(2)∵ED=EF,
∴2t=12-2t.
解得:t=3.
点评 本题主要考查的是一元二次方程的应用,根据四边形DFCE的面积=△ABC的面积-△ADE的面积-△DBF的面积=20cm2列关于t的方程是解题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目


 如图,∠AOB=55°,画出∠BOC的平分线OD,计算∠AOD的度数.
如图,∠AOB=55°,画出∠BOC的平分线OD,计算∠AOD的度数.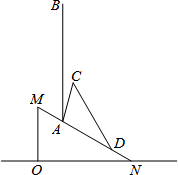 今年夏天我市出现厄尔尼诺现象极端天气,多地引发滑坡、山洪等严重自然灾害.如图所示,ON为水平线,斜坡MN的坡比为1:$\sqrt{3}$,斜坡上一棵大树树干AB(树干AB垂直于底面ON)被大风刮倾斜15°后折断倒在山坡上,树的顶部恰好接触到坡面,经测量,大树被折断部分与坡面所成的角∠ADC=30°,AD=8米,∠BAC=15°.
今年夏天我市出现厄尔尼诺现象极端天气,多地引发滑坡、山洪等严重自然灾害.如图所示,ON为水平线,斜坡MN的坡比为1:$\sqrt{3}$,斜坡上一棵大树树干AB(树干AB垂直于底面ON)被大风刮倾斜15°后折断倒在山坡上,树的顶部恰好接触到坡面,经测量,大树被折断部分与坡面所成的角∠ADC=30°,AD=8米,∠BAC=15°.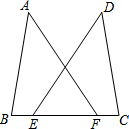 如图,点E、F在BC上,BE=CF,AB=DC,AF=DE.求证:∠B=∠C.
如图,点E、F在BC上,BE=CF,AB=DC,AF=DE.求证:∠B=∠C.