题目内容
16．若式子（2a-b）0+4a-2无意义，且2a+b=2，试求整式（2a-b）2-2（a-b）•（2a+b）+（2a+b）2的值．分析 直接利用零指数幂的性质得出2a-b=0，或负整数指数幂的底数为0，进而得出关于a，b方程组，求出a、b即可代入得出答案即可．
解答 解：∵式子（2a-b）0+4a-2无意义，
∴2a-b=0，或a=0，
当2a-b=0时，则$\left\{\begin{array}{l}{2a-b=0}\\{2a+b=2}\end{array}\right.$，解得：$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=1}\end{array}\right.$，（2a-b）2-2（a-b）•（2a+b）+（2a+b）2=6；
当a=0时，2a+b=2，解得：b=2，（2a-b）2-2（a-b）•（2a+b）+（2a+b）2=4+8+4=16．
点评 此题主要考查了零指数幂的性质，负整数指数幂的性质以及二元一次方程组的解法，正确解二元一次方程组是解题关键．
练习册系列答案
相关题目
在Rt△ABC中，∠C=90°，BC=$\sqrt{3}$，∠B的平分线BD=2$\sqrt{3}$，求∠DBC和∠ABD的度数．
如图，在Rt△ACB中，∠ACB=Rt∠，D是AB的中点，tan∠ACD=$\frac{1}{3}$，求∠A，∠B的度数（精确到1′）
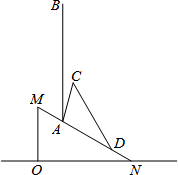今年夏天我市出现厄尔尼诺现象极端天气，多地引发滑坡、山洪等严重自然灾害．如图所示，ON为水平线，斜坡MN的坡比为1：$\sqrt{3}$，斜坡上一棵大树树干AB（树干AB垂直于底面ON）被大风刮倾斜15°后折断倒在山坡上，树的顶部恰好接触到坡面，经测量，大树被折断部分与坡面所成的角∠ADC=30°，AD=8米，∠BAC=15°．