题目内容
13. 如图:
如图:①图中两直线的交点坐标可以看作方程组$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{5}{2}x-2}\end{array}\right.$的解;
②两条直线与纵轴所围成的三角形面积为3;
③设直线l1所表示的数值为y1,设直线12所表示的函数值为y2.
当x>-1时,y1>0;
当x>$\frac{4}{5}$时,y2>0;
当x>$\frac{4}{5}$时,y1>0,y2>0同时成立;
当x为何值时,y1>y2.
分析 ①先利用待定系数法求出两直线的解析式,然后根据两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;
②利用三角形的面积求得答案即可;
③利用图象直接得出答案即可.
解答 解:①设直线l1的解析式为y=kx+b,
把(2,3)、(0,1)分别代入得$\left\{\begin{array}{l}{2k+b=3}\\{b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{b=1}\end{array}\right.$,
所以直线l1的解析式为y=x+1,
设直线l2的解析式为y=mx+n,
把(2,3)、(0,-2)分别代入得$\left\{\begin{array}{l}{2m+n=3}\\{n=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=\frac{5}{2}}\\{n=-2}\end{array}\right.$,
所以直线l2的解析式为y=$\frac{5}{2}$x-2,
所以两直线l1,l2的交点坐标可以看作方程组$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{5}{2}x-2}\end{array}\right.$的解.
②三角形面积为$\frac{1}{2}$×3×2=3;
③当x>-1时,y1>0;
当x>$\frac{4}{5}$时,y2>0;
当x>$\frac{4}{5}$时,y1>0,y2>0同时成立;
当x<2时,y1>y2.
故答案为:$\left\{\begin{array}{l}{y=x+1}\\{y=\frac{5}{2}x-2}\end{array}\right.$,3,>-1,>$\frac{4}{5}$,>$\frac{4}{5}$,x<2时.
点评 此题考查一次函数与二元一次方程组,一元一次不等式的关系,函数图象交点坐标为两函数解析式组成的方程组的解,利用数形结合的思想解决问题.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案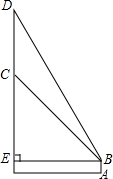 如图,在一座楼房墙上有一面广告牌,小明站在楼房正面距离该楼房12米的A处,自B点看正前方的广告牌上端D处的仰角为60°,下端C处的仰角为45°.求该广告牌上下两端之间的距离CD.(结果精确到0.1米)
如图,在一座楼房墙上有一面广告牌,小明站在楼房正面距离该楼房12米的A处,自B点看正前方的广告牌上端D处的仰角为60°,下端C处的仰角为45°.求该广告牌上下两端之间的距离CD.(结果精确到0.1米)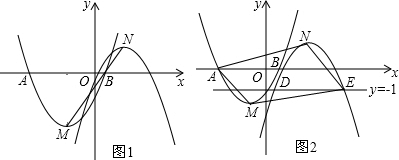
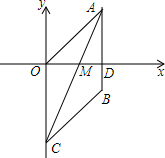 如图,在平面直角坐标系中,A(8,6),C(0,-10),AC=CO,直线AC交x轴于点M,将△AOC沿直线AC翻折,使得点O落在点B处,连接AB交x轴于D,动点P从点O出发,以2个单位长度/秒的速度沿射线OA运动;同时动点Q从A出发以每秒1个单位的速度沿射线AB运动.
如图,在平面直角坐标系中,A(8,6),C(0,-10),AC=CO,直线AC交x轴于点M,将△AOC沿直线AC翻折,使得点O落在点B处,连接AB交x轴于D,动点P从点O出发,以2个单位长度/秒的速度沿射线OA运动;同时动点Q从A出发以每秒1个单位的速度沿射线AB运动.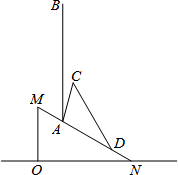 今年夏天我市出现厄尔尼诺现象极端天气,多地引发滑坡、山洪等严重自然灾害.如图所示,ON为水平线,斜坡MN的坡比为1:$\sqrt{3}$,斜坡上一棵大树树干AB(树干AB垂直于底面ON)被大风刮倾斜15°后折断倒在山坡上,树的顶部恰好接触到坡面,经测量,大树被折断部分与坡面所成的角∠ADC=30°,AD=8米,∠BAC=15°.
今年夏天我市出现厄尔尼诺现象极端天气,多地引发滑坡、山洪等严重自然灾害.如图所示,ON为水平线,斜坡MN的坡比为1:$\sqrt{3}$,斜坡上一棵大树树干AB(树干AB垂直于底面ON)被大风刮倾斜15°后折断倒在山坡上,树的顶部恰好接触到坡面,经测量,大树被折断部分与坡面所成的角∠ADC=30°,AD=8米,∠BAC=15°. 已知:如图,M为△ABC的边BC的中点,AT平分∠BAC,交BC于T,ME∥AT交CA的延长线于E.求证:BD=CE.
已知:如图,M为△ABC的边BC的中点,AT平分∠BAC,交BC于T,ME∥AT交CA的延长线于E.求证:BD=CE. 如图,已知四边形ABCD的对角线交于点O,∠BAC=∠BDC.
如图,已知四边形ABCD的对角线交于点O,∠BAC=∠BDC.