题目内容
10. 如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是$\widehat{AB}$的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为( )
如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是$\widehat{AB}$的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为( )| A. | 2π-4 | B. | 4π-8 | C. | 2π-8 | D. | 4π-4 |
分析 连结OC,根据勾股定理可求OC的长,根据题意可得出阴影部分的面积=扇形BOC的面积-三角形ODC的面积,依此列式计算即可求解.
解答 解:∵在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是$\widehat{AB}$的中点,
∴∠COD=45°,
∴OC=$\sqrt{(2\sqrt{2})^{2}+(2\sqrt{2})^{2}}$=4,
∴阴影部分的面积=扇形BOC的面积-三角形ODC的面积
=$\frac{45}{360}$×π×42-$\frac{1}{2}$×(2$\sqrt{2}$)2
=2π-4.
故选:A.
点评 考查了正方形的性质和扇形面积的计算,解题的关键是得到扇形半径的长度.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
20.下列运算正确的是( )
| A. | $\sqrt{6}$-$\sqrt{3}$=$\sqrt{3}$ | B. | $\sqrt{(-3)^{2}}$=-3 | C. | a•a2=a2 | D. | (2a3)2=4a6 |
18. 如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P=40°,则∠ABC的度数为( )
如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P=40°,则∠ABC的度数为( )
 如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P=40°,则∠ABC的度数为( )
如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P=40°,则∠ABC的度数为( )| A. | 20° | B. | 25° | C. | 40° | D. | 50° |
5.下列运算正确的是( )
| A. | 8a-a=8 | B. | (-a)4=a4 | C. | a3•a2=a6 | D. | (a-b)2=a2-b2 |
20.已知函数y=(k-1)x2-4x+4与x轴只有一个交点,则k的取值范围是( )
| A. | k≤2且k≠1 | B. | k<2且k≠1 | C. | k=2 | D. | k=2或1 |
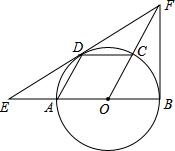 如图,AB是⊙O的直径,点C、D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA延长线与OC延长线于点E、F,连接BF.
如图,AB是⊙O的直径,点C、D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA延长线与OC延长线于点E、F,连接BF.