题目内容
1.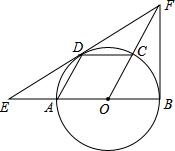 如图,AB是⊙O的直径,点C、D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA延长线与OC延长线于点E、F,连接BF.
如图,AB是⊙O的直径,点C、D在圆上,且四边形AOCD是平行四边形,过点D作⊙O的切线,分别交OA延长线与OC延长线于点E、F,连接BF.(1)求证:BF是⊙O的切线;
(2)已知圆的半径为1,求EF的长.
分析 (1)先证明四边形AOCD是菱形,从而得到∠AOD=∠COD=60°,再根据切线的性质得∠FDO=90°,接着证明△FDO≌△FBO得到∠ODF=∠OBF=90°,然后根据切线的判定定理即可得到结论;
(2)在Rt△OBF中,利用60度的正切的定义求解.
解答 (1)证明:连结OD,如图, ∵四边形AOCD是平行四边形,
∵四边形AOCD是平行四边形,
而OA=OC,
∴四边形AOCD是菱形,
∴△OAD和△OCD都是等边三角形,
∴∠AOD=∠COD=60°,
∴∠FOB=60°,
∵EF为切线,
∴OD⊥EF,
∴∠FDO=90°,
在△FDO和△FBO中
$\left\{\begin{array}{l}{OD=OB}\\{∠FOD=∠FOB}\\{FO=FO}\end{array}\right.$,
∴△FDO≌△FBO,
∴∠ODF=∠OBF=90°,
∴OB⊥BF,
∴BF是⊙O的切线;
(2)解:在Rt△OBF中,∵∠FOB=60°,
而tan∠FOB=$\frac{BF}{OB}$,
∴BF=1×tan60°=$\sqrt{3}$.
∵∠E=30°,
∴EF=2BF=2$\sqrt{3}$.
点评 本题考查了切线的判断与性质:圆的切线垂直于经过切点的半径;经过半径的外端且垂直于这条半径的直线是圆的切线.有切线时,常常“遇到切点连圆心得半径”.

练习册系列答案
相关题目
11.关于$\sqrt{12}$的叙述,错误的是( )
| A. | $\sqrt{12}$是有理数 | B. | 面积为12的正方形边长是$\sqrt{12}$ | ||
| C. | $\sqrt{12}$=2$\sqrt{3}$ | D. | 在数轴上可以找到表示$\sqrt{12}$的点 |
6.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (a2)3=a5 | C. | (-2a2b)3=-8a6b3 | D. | (2a+1)2=4a2+2a+1 |
13.某班7名女生的体重(单位:kg)分别是35、37、38、40、42、42、74,这组数据的众数是( )
| A. | 74 | B. | 44 | C. | 42 | D. | 40 |





 如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是$\widehat{AB}$的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为( )
如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是$\widehat{AB}$的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为( )