题目内容
18. 如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P=40°,则∠ABC的度数为( )
如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC.若∠P=40°,则∠ABC的度数为( )| A. | 20° | B. | 25° | C. | 40° | D. | 50° |
分析 利用切线的性质和直角三角形的两个锐角互余的性质得到圆心角∠PAO的度数,然后利用圆周角定理来求∠ABC的度数.
解答  解:如图,∵AB是⊙O的直径,直线PA与⊙O相切于点A,
解:如图,∵AB是⊙O的直径,直线PA与⊙O相切于点A,
∴∠PAO=90°.
又∵∠P=40°,
∴∠POA=50°,
∴∠ABC=$\frac{1}{2}$∠POA=25°.
故选:B.
点评 本题考查了切线的性质,圆周角定理.圆的切线垂直于经过切点的半径.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
6.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (a2)3=a5 | C. | (-2a2b)3=-8a6b3 | D. | (2a+1)2=4a2+2a+1 |
13.某班7名女生的体重(单位:kg)分别是35、37、38、40、42、42、74,这组数据的众数是( )
| A. | 74 | B. | 44 | C. | 42 | D. | 40 |
3.下列四个数中,最小的正数是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
10. 如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是$\widehat{AB}$的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为( )
如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是$\widehat{AB}$的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为( )
 如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是$\widehat{AB}$的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为( )
如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是$\widehat{AB}$的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为( )| A. | 2π-4 | B. | 4π-8 | C. | 2π-8 | D. | 4π-4 |
8.已知一元二次方程x2+bx-6=0有一个根为2,则另一根为( )
| A. | 2 | B. | -3 | C. | 4 | D. | 3 |
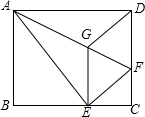 如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.