题目内容
15.如图,抛物线y=ax2+2x-3与x轴交于A、B两点,且B(1,0)(1)求抛物线的解析式和点A的坐标;
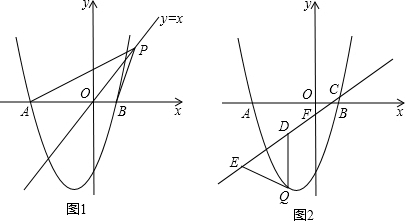
(2)如图1,点P是直线y=x上的动点,当直线y=x平分∠APB时,求点P的坐标;
(3)如图2,已知直线y=$\frac{2}{3}$x-$\frac{4}{9}$分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
分析 (1)把B点坐标代入抛物线解析式可求得a的值,可求得抛物线解析式,再令y=0,可解得相应方程的根,可求得A点坐标;
(2)当点P在x轴上方时,连接AP交y轴于点B′,可证△OBP≌△OB′P,可求得B′坐标,利用待定系数法可求得直线AP的解析式,联立直线y=x,可求得P点坐标;当点P在x轴下方时,同理可求得∠BPO=∠B′PO,又∠B′PO在∠APO的内部,可知此时没有满足条件的点P;
(3)过Q作QH⊥DE于点H,由直线CF的解析式可求得点C、F的坐标,结合条件可求得tan∠QDH,可分别用DQ表示出QH和DH的长,分DQ=DE和DQ=QE两种情况,分别用DQ的长表示出△QDE的面积,再设出点Q的坐标,利用二次函数的性质可求得△QDE的面积的最大值.
解答 解:
(1)把B(1,0)代入y=ax2+2x-3,
可得a+2-3=0,解得a=1,
∴抛物线解析式为y=x2+2x-3,
令y=0,可得x2+2x-3=0,解得x=1或x=-3,
∴A点坐标为(-3,0);
(2)若y=x平分∠APB,则∠APO=∠BPO,
如图1,若P点在x轴上方,PA与y轴交于点B′,
由于点P在直线y=x上,可知∠POB=∠POB′=45°,
在△BPO和△B′PO中
$\left\{\begin{array}{l}{∠POB=∠PO{B}^{′}}\\{OP=OP}\\{∠BPO=∠{B}^{′}PO}\end{array}\right.$,
∴△BPO≌△B′PO(ASA),
∴BO=B′O=1,
设直线AP解析式为y=kx+b,把A、B′两点坐标代入可得
$\left\{\begin{array}{l}{-3k+b=0}\\{b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=1}\end{array}\right.$,
∴直线AP解析式为y=$\frac{1}{3}$x+1,
联立$\left\{\begin{array}{l}{y=x}\\{y=\frac{1}{3}x+1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=\frac{3}{2}}\end{array}\right.$,
∴P点坐标为($\frac{3}{2}$,$\frac{3}{2}$);
若P点在x轴下方时,同理可得△AOP≌△B′OP,
∴∠BPO=∠B′PO,
又∠B′PO在∠APO的内部,
∴∠APO≠∠BPO,即此时没有满足条件的P点,
综上可知P点坐标为($\frac{3}{2}$,$\frac{3}{2}$);
(3)如图2,作QH⊥CF,交CF于点H,
∵CF为y=$\frac{2}{3}$x-$\frac{4}{9}$,
∴可求得C($\frac{2}{3}$,0),F(0,-$\frac{4}{9}$),
∴tan∠OFC=$\frac{OC}{OF}$=$\frac{3}{2}$,
∵DQ∥y轴,
∴∠QDH=∠MFD=∠OFC,
∴tan∠HDQ=$\frac{3}{2}$,
不妨设DQ=t,DH=$\frac{2}{\sqrt{13}}$t,HQ=$\frac{3}{\sqrt{13}}$t,
∵△QDE是以DQ为腰的等腰三角形,
∴若DQ=DE,则S△DEQ=$\frac{1}{2}$DE•HQ=$\frac{1}{2}$×$\frac{3}{\sqrt{13}}$t×t=$\frac{3\sqrt{13}}{26}$t2,
若DQ=QE,则S△DEQ=$\frac{1}{2}$DE•HQ=$\frac{1}{2}$×2DH•HQ=$\frac{1}{2}$×$\frac{4}{\sqrt{13}}$t×$\frac{3}{\sqrt{13}}$t=$\frac{6}{13}$t2,
∵$\frac{3\sqrt{13}}{26}$t2<$\frac{6}{13}$t2,
∴当DQ=QE时△DEQ的面积比DQ=DE时大.
设Q点坐标为(x,x2+2x-3),则D(x,$\frac{2}{3}$x-$\frac{4}{9}$),
∵Q点在直线CF的下方,
∴DQ=t=$\frac{2}{3}$x-$\frac{4}{9}$-(x2+2x-3)=-x2-$\frac{4}{3}$x+$\frac{23}{9}$,
当x=-$\frac{2}{3}$时,tmax=3,
∴(S△DEQ)max=$\frac{6}{13}$t2=$\frac{54}{13}$,
即以QD为腰的等腰三角形的面积最大值为$\frac{54}{13}$.
点评 本题主要考查二次函数的综合应用,涉及知识点有待定系数法、角平分线的定义、全等三角形的判定和性质、三角形的面积、等腰三角形的性质、二次函数的性质及分类讨论等.在(2)中确定出直线AP的解析式是解题的关键,在(3)中利用DQ表示出△QDE的面积是解题的关键.本题考查知识点较多,综合性较强,计算量大,难度较大.

 应用题作业本系列答案
应用题作业本系列答案| A. | a2•a3=a6 | B. | (a2)3=a5 | C. | (-2a2b)3=-8a6b3 | D. | (2a+1)2=4a2+2a+1 |
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
 如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是$\widehat{AB}$的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为( )
如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是$\widehat{AB}$的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2$\sqrt{2}$时,则阴影部分的面积为( )| A. | 2π-4 | B. | 4π-8 | C. | 2π-8 | D. | 4π-4 |
| A. | $\frac{1}{x+1}$ | B. | $\frac{x+1}{x}$ | C. | x+1 | D. | x-1 |
 如图,已知∠1=60°,如果CD∥BE,那么∠B的度数为( )
如图,已知∠1=60°,如果CD∥BE,那么∠B的度数为( )| A. | 70° | B. | 100° | C. | 110° | D. | 120° |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 2 | D. | 4 |
 如图,是由四个大小相同的小正方体拼成的几何体,则这个几何体的左视图是( )
如图,是由四个大小相同的小正方体拼成的几何体,则这个几何体的左视图是( )


