题目内容
15.先化简,再求值:(1-$\frac{x}{x-1}$)÷$\frac{1}{{x}^{2}-x}$,其中x=2.分析 根据运算顺序,先算括号里面的,再将除法转化为乘法计算可得.
解答 解:原式=-$\frac{1}{x-1}$•x(x-1)
=-x,
当x=2时,原式=-2.
点评 本题考查了分式的化简求值,掌握分式的通分和约分是解题的关键.

练习册系列答案
相关题目
10.对于两个不相等的实数a、b,我们规定符号max{a,b}表示a、b中较大的数,如:max{2,4}=4.按照这个规定.方程max{x,-x}=$\frac{2x+1}{x}$的解为( )
| A. | $1-\sqrt{2}$ | B. | $2-\sqrt{2}$ | C. | $1-\sqrt{2}$或$1+\sqrt{2}$ | D. | $1+\sqrt{2}$或-1 |
20. 如图所示,AB∥CD,∠BEF和∠DFE的角平分线交于点G,∠1=100°,则∠2的度数是( )
如图所示,AB∥CD,∠BEF和∠DFE的角平分线交于点G,∠1=100°,则∠2的度数是( )
 如图所示,AB∥CD,∠BEF和∠DFE的角平分线交于点G,∠1=100°,则∠2的度数是( )
如图所示,AB∥CD,∠BEF和∠DFE的角平分线交于点G,∠1=100°,则∠2的度数是( )| A. | 15° | B. | 20 | C. | 30° | D. | 40 |
7.济宁市某经济开发区,今年一月份工业产值达10亿元,第一季度总产值为75亿元,二、三月平均每月增长率是多少,若设平均每月的增长率为x,根据题意,可列方程为( )
| A. | 10(1+x)2=75 | B. | 10+10(1+x)+10(1+x)2=75 | ||
| C. | 10(1+x)+10(1+x)2=75 | D. | 10+10(1+x)2=75 |
4. 如图,在?ABCD中,∠ABC,∠BCD的平分线BE,CF分别与AD相交于点E、F,BE与CF相交于点G,若AB=3,BC=5,CF=2,则BE的长为( )
如图,在?ABCD中,∠ABC,∠BCD的平分线BE,CF分别与AD相交于点E、F,BE与CF相交于点G,若AB=3,BC=5,CF=2,则BE的长为( )
 如图,在?ABCD中,∠ABC,∠BCD的平分线BE,CF分别与AD相交于点E、F,BE与CF相交于点G,若AB=3,BC=5,CF=2,则BE的长为( )
如图,在?ABCD中,∠ABC,∠BCD的平分线BE,CF分别与AD相交于点E、F,BE与CF相交于点G,若AB=3,BC=5,CF=2,则BE的长为( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 4$\sqrt{2}$ | D. | 5 |
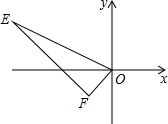 如图,点E(-4,2),F(-1,-1),以点O为位似中心,在点O的另一侧,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为(2,-1).
如图,点E(-4,2),F(-1,-1),以点O为位似中心,在点O的另一侧,按比例尺1:2,把△EFO缩小,则点E的对应点E′的坐标为(2,-1).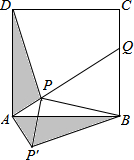 如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q. 已知:x为实数,[x]表示不超过x的最大整数,如[3.14]=3,[1]=1,[-1.2]=-2.请你在学习,理解上述定义的基础上,解决下列问题:设函数y=x-[x].
已知:x为实数,[x]表示不超过x的最大整数,如[3.14]=3,[1]=1,[-1.2]=-2.请你在学习,理解上述定义的基础上,解决下列问题:设函数y=x-[x]. 在一条公路上依次有A、B、C三个车站,甲、乙两车同时分别从A、B车站出发,匀速开往C车站,最终到达C车站,设甲、乙两车行驶x(h)后,与B车站的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.
在一条公路上依次有A、B、C三个车站,甲、乙两车同时分别从A、B车站出发,匀速开往C车站,最终到达C车站,设甲、乙两车行驶x(h)后,与B车站的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.