题目内容
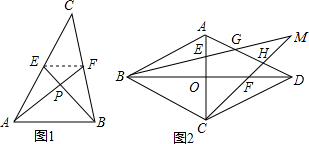
4. 如图,在?ABCD中,∠ABC,∠BCD的平分线BE,CF分别与AD相交于点E、F,BE与CF相交于点G,若AB=3,BC=5,CF=2,则BE的长为( )
如图,在?ABCD中,∠ABC,∠BCD的平分线BE,CF分别与AD相交于点E、F,BE与CF相交于点G,若AB=3,BC=5,CF=2,则BE的长为( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 4$\sqrt{2}$ | D. | 5 |
分析 根据平行四边形两组对边分别平行可得∠ABC+∠BCD=180°,再根据角平分线的性质可得∠EBC+∠FCB=90°,可得BE⊥CF;过A作AM∥FC,∠BC于M,证明△ABE是等腰三角形,进而得到BO=EO,再利用勾股定理计算出EO的长,进而可得答案.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABC、∠BCD的平分线BE、CF分别与AD相交于点E、F,
∴∠EBC+∠FCB=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠DCB=90°
∴EB⊥FC;
过A作AM∥FC,交BC于M,如图所示:
∵AM∥FC,
∴∠AOB=∠FGB,
∵EB⊥FC,
∴∠FGB=90°,
∴∠AOB=90°,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∵AD∥BC,
∴∠AEB=∠CBE,
∴∠ABE=∠AEB,
∴AB=AE=3,
∵AO⊥BE,
∴BO=EO,
在△AOE和△MOB中,
$\left\{\begin{array}{l}{∠AEO=∠MBO}&{\;}\\{BO=EO}&{\;}\\{∠AOE=∠BOM}&{\;}\end{array}\right.$,
∴△AOE≌△MOB(ASA),
∴AO=MO,
∵AF∥CM,AM∥FC,
∴四边形AMCF是平行四边形,
∴AM=FC=2,
∴AO=1,
∴EO=$\sqrt{A{E}^{2}-A{O}^{2}}$=2$\sqrt{2}$,
∴BE=4$\sqrt{2}$;
故选:C.
点评 此题主要考查了平行四边形的性质与判定、全等三角形的判定与性质、等腰三角形的判定和性质;证明AO=MO,BO=EO是解决问题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
14.下列计算正确的是( )
| A. | (3a)2=6a2 | B. | (-3)-2=6 | C. | $\sqrt{(-2)^{2}}$=-2 | D. | $\sqrt{18}$+$\sqrt{2}$=4$\sqrt{2}$ |
12.在平面直角坐标系中,下列各点在第四象限的是( )
| A. | (2,1) | B. | (2,-1) | C. | (-2,1) | D. | (-2,-1) |
9.|-2|=( )
| A. | 2 | B. | -2 | C. | ±2 | D. | $\frac{1}{2}$ |
16.下列运算中,正确的是( )
| A. | x3•x2=x6 | B. | (x2)3=x6 | C. | x2+x3=x5 | D. | (2x2)3=6x6 |
 将如图所示的Rt△ABC绕直角边AB旋转一周,则所得几何体的主视图为( )
将如图所示的Rt△ABC绕直角边AB旋转一周,则所得几何体的主视图为( )



 如图,抛物线y=ax2+bx-3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=-$\frac{1}{3}$x+1与y轴交于点D.
如图,抛物线y=ax2+bx-3(a≠0)的顶点为E,该抛物线与x轴交于A、B两点,与y轴交于点C,且BO=OC=3AO,直线y=-$\frac{1}{3}$x+1与y轴交于点D.