��Ŀ����
3�� ��֪��xΪʵ����[x]��ʾ������x�������������[3.14]=3��[1]=1��[-1.2]=-2��������ѧϰ��������������Ļ����ϣ�����������⣺�躯��y=x-[x]��
��֪��xΪʵ����[x]��ʾ������x�������������[3.14]=3��[1]=1��[-1.2]=-2��������ѧϰ��������������Ļ����ϣ�����������⣺�躯��y=x-[x]����1����x=2.15ʱ����y=x-[x]��ֵ��
��2����0��x��2������y=x-[x]�ı���ʽ������������ͼ��
��3���ڣ�2���������£�ƽ��ֱ������ϵxOy�У���OΪԲ�ģ�rΪ�뾶��Բ����r��2����Բ�뺯��y=x-[x]ǡ��һ�������㣬��ֱ��д��r��ȡֵ��Χ��
���� ��1������[x]�Ķ�����м��㼴�ɣ�
��2������֪������0��x��1��1��x��2���з������ۣ��ɴ˿�������ۣ�
��3�����ݣ�2���������£���������Χ����ʽ�鼴�ɣ�
���  �⣺��1����x=2.15ʱ
�⣺��1����x=2.15ʱ
y=x-[x]
=2.15-[2.15]
=2.15-2
=0.15��
��2���ٵ�0��x��1ʱ��[x]=0��
��y=x-[x]��
��y=x��
�ڵ�1��x��2ʱ��[x]=1��
��y=x-[x]��
��y=x-1��
��3���ڣ�2���������£�����y=x-[x]��ͼ��OA=$\sqrt{2}$��
�ٵ�0��x��1ʱ��0��r��1����r��0A=$\sqrt{2}$����0��r��1��
�ڵ�1��x��2ʱ��1��r��2����$\sqrt{2}$��r$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$��
�֡�r��2��
��$\sqrt{2}$��r��2��
����������0��r��1��$\sqrt{2}$��r��2��
���� ������Ҫ�����˺���ֵ�����ǻ����⣬ע���������⣬����Ĺؼ����ܹ����ν��˼��ͷ���˼��ĺ������ã�

��ϰ��ϵ�д�
 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�
�����Ŀ
14�����м�����ȷ���ǣ�������
| A�� | ��3a��2=6a2 | B�� | ��-3��-2=6 | C�� | $\sqrt{��-2��^{2}}$=-2 | D�� | $\sqrt{18}$+$\sqrt{2}$=4$\sqrt{2}$ |
11�����м�����Ϊa5���ǣ�������
| A�� | ��a3��2 | B�� | a3+a2 | C�� | a6-a1 | D�� | a3•a2 |
18�����и����б�1С�����ǣ�������
| A�� | $\sqrt{3}$ | B�� | $\sqrt{2}$ | C�� | 1 | D�� | 0 |
12����ƽ��ֱ������ϵ�У����и����ڵ��������ǣ�������
| A�� | ��2��1�� | B�� | ��2��-1�� | C�� | ��-2��1�� | D�� | ��-2��-1�� |
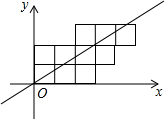 ��ͼ��10���߳�Ϊ1����������ͼ�ڷ���ƽ��ֱ������ϵ�У�����ԭ���һ��ֱ��l����10�������ηֳ������ȵ������֣����ֱ��l�Ľ���ʽΪy=$\frac{9}{14}$x��
��ͼ��10���߳�Ϊ1����������ͼ�ڷ���ƽ��ֱ������ϵ�У�����ԭ���һ��ֱ��l����10�������ηֳ������ȵ������֣����ֱ��l�Ľ���ʽΪy=$\frac{9}{14}$x�� ��ͼ������ABCD�У���O��BC�ϣ�OB=2OC=2����OΪԲ��OB�ij��뾶������������ǡ�þ�����D����ͼ����Ӱ���ֵ����Ϊ$\frac{2��}{3}$-$\sqrt{3}$��
��ͼ������ABCD�У���O��BC�ϣ�OB=2OC=2����OΪԲ��OB�ij��뾶������������ǡ�þ�����D����ͼ����Ӱ���ֵ����Ϊ$\frac{2��}{3}$-$\sqrt{3}$��