题目内容
6.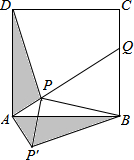 如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.(1)求证:△APP′是等腰直角三角形;
(2)判断△BPP′的形状,并求∠BPQ的度数;
(3)求正方形ABCD的边AB的长.
分析 (1)根据旋转的性质可知,△APD≌△AP′B,所以AP=AP′,∠PAD=∠P′AB,因为∠PAD+∠PAB=90°,所以∠P′AB+∠PAB=90°,即∠PAP′=90°,故△APP′是等腰直角三角形;
(2)先根据勾股定理逆定理判断△BPP′是直角三角形,得出∠P′PB=90°,由(1)知△APP′是等腰直角三角形,那么∠APP′=45°,再根据平角定义即可求出∠BPQ的度数;
(3)作BE⊥AQ,垂足为E,先由∠BPQ=45°,PB=2$\sqrt{2}$,求出PE=BE=2,然后在Rt△ABE中,运用勾股定理求出AB.
解答 解:(1)∵△ADP沿点A旋转至△ABP′,
∴根据旋转的性质可知,△APD≌△AP′B,
∴AP=AP′,∠PAD=∠P′AB,
∵∠PAD+∠PAB=90°,
∴∠P′AB+∠PAB=90°,
即∠PAP′=90°,
∴△APP′是等腰直角三角形;
(2)由(1)知∠PAP′=90°,AP=AP′=1,
∴PP′=$\sqrt{2}$,
∵P′B=PD=$\sqrt{10}$,PB=2$\sqrt{2}$,
∴P′B2=PP′2+PB2,
∴∠P′PB=90°,
∵△APP′是等腰直角三角形,
∴∠APP′=45°,
∴∠BPQ=180°-90°-45°=45°;
(3)如图,作BE⊥AQ,垂足为E,
∵∠BPQ=45°,PB=2$\sqrt{2}$,
∴PE=BE=2,
∴AE=AP+PE=1+2=3,
∴AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
即正方形ABCD的边AB的长为$\sqrt{13}$.
点评 本题是四边形综合题,考查了旋转的性质、等腰直角三角形的判定与性质、勾股定理及其逆定理等知识,难度适中,作BE⊥AQ于E,构造直角三角形是解决问题(3)的关键.

| A. | 880名考生 | B. | 200名考生 | ||
| C. | 880名考生的数学成绩 | D. | 200名考生的数学成绩 |
| A. | (3a)2=6a2 | B. | (-3)-2=6 | C. | $\sqrt{(-2)^{2}}$=-2 | D. | $\sqrt{18}$+$\sqrt{2}$=4$\sqrt{2}$ |
| A. | (a3)2 | B. | a3+a2 | C. | a6-a1 | D. | a3•a2 |
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 0 |
| A. | x3•x2=x6 | B. | (x2)3=x6 | C. | x2+x3=x5 | D. | (2x2)3=6x6 |
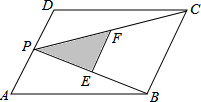 如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,若△PEF的面积S1=1,则?ABCD的面积S=8.
如图,P为平行四边形ABCD边AD上一点,E、F分别为PB、PC的中点,若△PEF的面积S1=1,则?ABCD的面积S=8.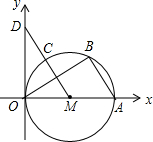 如图,直径为OA的圆M与x轴交于点O,A,点B,C把半圆OA分为三等份,连接MC并延长交y轴于点D.
如图,直径为OA的圆M与x轴交于点O,A,点B,C把半圆OA分为三等份,连接MC并延长交y轴于点D.