题目内容
10.对于两个不相等的实数a、b,我们规定符号max{a,b}表示a、b中较大的数,如:max{2,4}=4.按照这个规定.方程max{x,-x}=$\frac{2x+1}{x}$的解为( )| A. | $1-\sqrt{2}$ | B. | $2-\sqrt{2}$ | C. | $1-\sqrt{2}$或$1+\sqrt{2}$ | D. | $1+\sqrt{2}$或-1 |
分析 分x<-x和x>-x两种情况将所求方程变形,求出解即可.
解答 解:当x<-x,即x<0时,所求方程变形为-x=$\frac{2x+1}{x}$,
去分母得:x2+2x+1=0,即(x+1)2=0,
解得:x1=x2=-1,
经检验x=-1是分式方程的解;
当x>-x,即x>0时,所求方程变形为x=$\frac{2x+1}{x}$,
去分母得:x2-2x-1=0,
代入公式得:x=$\frac{2±2\sqrt{2}}{2}$=1±$\sqrt{2}$,
解得:x3=1+$\sqrt{2}$,x4=1-$\sqrt{2}$(舍去),
经检验x=1+$\sqrt{2}$是分式方程的解,
综上,所求方程的解为1+$\sqrt{2}$或-1.
故选D
点评 此题考查了分式方程的解,弄清题中的新定义是解本题的关键.

练习册系列答案
相关题目
18.下列各数中比1小的数是( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 0 |
2.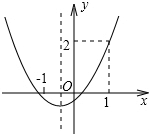 已知抛物线y=ax2+bx+c的图象如图所示,则下列结论中正确是( )
已知抛物线y=ax2+bx+c的图象如图所示,则下列结论中正确是( )
 已知抛物线y=ax2+bx+c的图象如图所示,则下列结论中正确是( )
已知抛物线y=ax2+bx+c的图象如图所示,则下列结论中正确是( )| A. | a+b+c>2 | B. | 2a-b<0 | C. | b<1 | D. | 3a+c>2 |
20.下列运算中正确的是( )
| A. | 5x-3x=2 | B. | x4•x=x5 | C. | (-a2)4=a6 | D. | 2x3÷$\frac{1}{2}$x=4x4 |
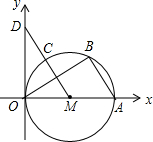 如图,直径为OA的圆M与x轴交于点O,A,点B,C把半圆OA分为三等份,连接MC并延长交y轴于点D.
如图,直径为OA的圆M与x轴交于点O,A,点B,C把半圆OA分为三等份,连接MC并延长交y轴于点D.
 将如图所示的Rt△ABC绕直角边AB旋转一周,则所得几何体的主视图为( )
将如图所示的Rt△ABC绕直角边AB旋转一周,则所得几何体的主视图为( )


