题目内容
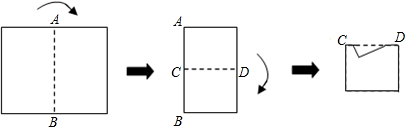
13.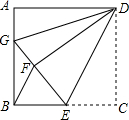 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,BF.
如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,BF.(1)求证:AG=FG;
(2)求cos∠BGE的值.
分析 (1)根据正方形的性质可得∠C=∠A=90°,DC=DA,根据翻折的性质可得DF=DC,∠DFE=∠C=90°,然后求出∠DFG=∠A=90°,DF=DA,再利用“HL”证明Rt△ADG和Rt△FDG全等,根据全等三角形对应边相等证明即可;
(2)先求出BE=EC=EF=6,设AG=x,表示出EG、BG,然后利用勾股定理列方程求出x的值,从而得到BG、EG,最后根据锐角的余弦等于邻边比斜边求解即可.
解答 (1)证明:∵正方形ABCD,
∴∠C=∠A=90°,DC=DA,
∵△DCE沿DE对折得到△DFE,
∴DF=DC,∠DFE=∠C=90°,
∴∠DFG=∠A=90°,DF=DA,
在Rt△ADG和Rt△FDG中,$\left\{\begin{array}{l}{DG=DG}\\{DF=DA}\end{array}\right.$,
∴Rt△ADG≌Rt△FDG(HL),
∴AG=FG;
(2)解:∵正方形ABCD中,AB=12,BE=EC,
∴BE=EC=EF=6,
设AG=x,则EG=6+x,
BG=12-x,
在Rt△BEG中,根据勾股定理得,EG2=BE2+BG2,
即(6+x)2=62+(12-x)2,
解得x=4,
所以,BG=12-4=8,
EG=6+4=10,
所以,cos∠BGE=$\frac{BG}{GE}$=$\frac{8}{10}$=$\frac{4}{5}$.
点评 本题考查了翻折变换的性质,正方形的性质,全等三角形的判定与性质,解直角三角形,翻折前后对应边相等,对应角相等,此类题目,难点在于利用勾股定理列出方程从而求出相关线段的长度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.计算(x+2)(x-2)结果正确的是( )
| A. | x2-4 | B. | x2-2 | C. | 4-x2 | D. | x2+2 |
1. 如图,△ABC内接于⊙O,∠C=30°,AB=4,则⊙O的半径为( )
如图,△ABC内接于⊙O,∠C=30°,AB=4,则⊙O的半径为( )
 如图,△ABC内接于⊙O,∠C=30°,AB=4,则⊙O的半径为( )
如图,△ABC内接于⊙O,∠C=30°,AB=4,则⊙O的半径为( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 5 |
8.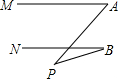 如图,直线MA∥NB,∠A=50°,∠B=20°,则∠P=( )度.
如图,直线MA∥NB,∠A=50°,∠B=20°,则∠P=( )度.
 如图,直线MA∥NB,∠A=50°,∠B=20°,则∠P=( )度.
如图,直线MA∥NB,∠A=50°,∠B=20°,则∠P=( )度.| A. | 20 | B. | 25 | C. | 30 | D. | 35 |
5.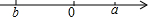 已知实数a、b在数轴上的对应位置如图所示,化简|a|-|b|+|a-b|-|b-a|结果为( )
已知实数a、b在数轴上的对应位置如图所示,化简|a|-|b|+|a-b|-|b-a|结果为( )
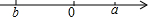 已知实数a、b在数轴上的对应位置如图所示,化简|a|-|b|+|a-b|-|b-a|结果为( )
已知实数a、b在数轴上的对应位置如图所示,化简|a|-|b|+|a-b|-|b-a|结果为( )| A. | a+b | B. | 3a-3b | C. | a-b | D. | a-3b |
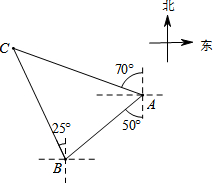 如图,国家规定休渔期间,我国渔政船在A处发现南偏西50°方向距A处20海里的点B处有一艘可疑船只,可疑船只正沿北偏西25°方向航行,我国渔政船立即沿北偏西70°方向前去拦截,经过1.5小时刚好在C处拦截住可疑船只,求该可疑船只航行的平均速度.
如图,国家规定休渔期间,我国渔政船在A处发现南偏西50°方向距A处20海里的点B处有一艘可疑船只,可疑船只正沿北偏西25°方向航行,我国渔政船立即沿北偏西70°方向前去拦截,经过1.5小时刚好在C处拦截住可疑船只,求该可疑船只航行的平均速度.