题目内容
1. 如图,△ABC内接于⊙O,∠C=30°,AB=4,则⊙O的半径为( )
如图,△ABC内接于⊙O,∠C=30°,AB=4,则⊙O的半径为( )| A. | 2$\sqrt{2}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 5 |
分析 连结BO并延长,交⊙O于D,根据同弧所对的圆周角相等得出∠D=∠C=30°.由直径所对的圆周角圆周角是直角得出∠BAD=90°,解直角△ABD求出BD=8,即可得出⊙O的半径为4.
解答  解:如图,连结BO并延长,交⊙O于D,则∠D=∠C=30°.
解:如图,连结BO并延长,交⊙O于D,则∠D=∠C=30°.
∵BD是⊙O的直径,
∴∠BAD=90°,
∴sin∠D=$\frac{AB}{BD}$,即$\frac{1}{2}$=$\frac{4}{BD}$,
∴BD=8,
∴⊙O的半径为4.
故选B.
点评 本题考查了三角形的外接圆与外心,圆周角定理,解直角三角形.准确作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
10.当2<a<3时,代数式|a-3|+|2-a|的值是( )
| A. | -1 | B. | 1 | C. | 5 | D. | -5 |
11.若(x+2)(x-1)=x2+mx+n成立,则m+n的值为( )
| A. | 1 | B. | -2 | C. | -1 | D. | 2 |
 如图,已知BD是矩形ABCD的对角线.
如图,已知BD是矩形ABCD的对角线.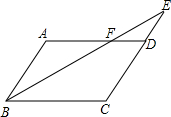 如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,且AF=2FD.
如图,?ABCD中,E是CD的延长线上一点,BE与AD交于点F,且AF=2FD.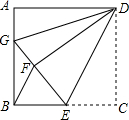 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,BF.
如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,BF.