题目内容
3.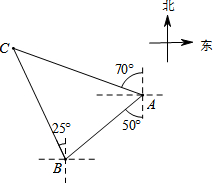 如图,国家规定休渔期间,我国渔政船在A处发现南偏西50°方向距A处20海里的点B处有一艘可疑船只,可疑船只正沿北偏西25°方向航行,我国渔政船立即沿北偏西70°方向前去拦截,经过1.5小时刚好在C处拦截住可疑船只,求该可疑船只航行的平均速度.
如图,国家规定休渔期间,我国渔政船在A处发现南偏西50°方向距A处20海里的点B处有一艘可疑船只,可疑船只正沿北偏西25°方向航行,我国渔政船立即沿北偏西70°方向前去拦截,经过1.5小时刚好在C处拦截住可疑船只,求该可疑船只航行的平均速度.(结果精确到个位,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
分析 作BD⊥AC于点D,由方向角得出∠ABD=30°、∠CBD=45°,在Rt△ABD中得BD=AB•sin∠CAB=10$\sqrt{3}$,在Rt△BCD中求得BC=BD÷cos∠CBD=10$\sqrt{6}$,再除以时间即可得.
解答 解:如图,作BD⊥AC于点D,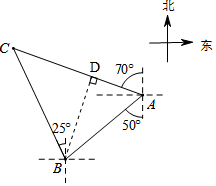
∵∠CBA=25°+50°=75°,∠CAB=(90°-70°)+(90°-50°)=60°,
∴∠ABD=30°,∠CBD=45°,
在Rt△ABD中,BD=AB•sin∠CAB=20×sin60°=20×$\frac{\sqrt{3}}{2}$=10$\sqrt{3}$,
在Rt△BCD中,BC=BD÷cos∠CBD=10$\sqrt{3}$÷cos45°=10$\sqrt{3}$÷$\frac{\sqrt{2}}{2}$=10$\sqrt{6}$,
∴可疑船只航行的平均速度$\frac{10\sqrt{6}}{1.5}$≈16(海里/小时).
点评 本题主要考查解直角三角形的应用-仰角俯角问题,根据题意构建合适的直角三角形,并熟练掌握三角函数的定义是解题的关键.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
14.不等式组$\left\{\begin{array}{l}{-3x>-6}\\{2x+1>0}\end{array}\right.$的解集是( )
| A. | x>2 | B. | x<-$\frac{1}{2}$ | C. | -$\frac{1}{2}$<x<2 | D. | $\frac{1}{2}$<x<2 |
8.某玩具厂生产一种玩具,据市场调查,若按每个玩具280元销售时,每月可销售300个,若销售单价每降低1元,每月可多售出2个,据统计,每个玩具的固定成本Q(元)与月销量y(个)满足如下关系:
(1)写出月销量y(个)与销售单价x(元)之间的函数关系式;
(2)求每个玩具的固定成本Q(元)与月销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的比例是多少?(用分数表示)
(4)若该厂这种玩具的月销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
| 月销量y(个) | … | 160 | 200 | 240 | 300 | … |
| 每个玩具的固定成本Q(元) | … | 60 | 48 | 40 | 32 | … |
(2)求每个玩具的固定成本Q(元)与月销量y(个)之间的函数关系式;
(3)若每个玩具的固定成本为30元,则它占销售单价的比例是多少?(用分数表示)
(4)若该厂这种玩具的月销量不超过400个,则每个玩具的固定成本至少为多少元?销售单价最低为多少元?
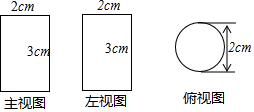 如图为一个几何体的三视图,
如图为一个几何体的三视图,
 如图,已知BD是矩形ABCD的对角线.
如图,已知BD是矩形ABCD的对角线.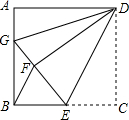 如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,BF.
如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,BF.