题目内容
14.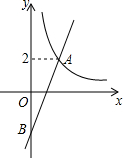 如图,在平面直角坐标系xOy中,双曲线y=$\frac{4}{x}$(x>0)与直线y=kx-k的交点为A(m,2).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{4}{x}$(x>0)与直线y=kx-k的交点为A(m,2).(1)求k的值;
(2)当x>0时,直接写出不等式kx-k>$\frac{4}{x}$的解集:x>2;
(3)设直线y=kx-k与y轴交于点B,若C是x轴上一点,且满足△ABC的面积是4,求点C的坐标.
分析 (1)利用待定系数法即可解决问题.
(2)观察图象,直线y=kx-k的图象在y=$\frac{4}{x}$的上方,由此可以写出不等式的解集.
(3)设点C坐标(m,0),直线y=2x-2与x轴的交点D坐标为(1,0),根据S△ABC=S△CDA+S△CDB=4,列出方程即可解决.
解答 解:(1)∵点A在双曲线y=$\frac{4}{x}$上,
∴2=$\frac{4}{m}$,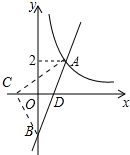
∴m=2,
∴点A(2,2).
∵点A在直线y=kx-k上,
∴2=2k-k,
∴k=2.
(2)由图象可知,x>0时,直接写出不等式kx-k>$\frac{4}{x}$的解集为x>2.
故答案为x>2.
(3)设点C坐标(m,0).
∵直线y=2x-2与x轴的交点D坐标为(1,0),
∴S△ABC=S△CDA+S△CDB=4,
∴$\frac{1}{2}$|m-1|•(2+2)=4,
∴m=3或-1.
∴点C坐标为(3,0)或(-1,0).
点评 本题考查反比例函数与一次函数图象的交点、待定系数法等知识,解题的关键是掌握待定系数法确定函数解析式,学会利用分割法求三角形面积,属于中考常考题型.

练习册系列答案
相关题目
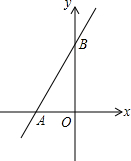 如图,平面直角坐标系中,点O为坐标原点,一次函数的图象过点(-1,4)与点(3,12).
如图,平面直角坐标系中,点O为坐标原点,一次函数的图象过点(-1,4)与点(3,12).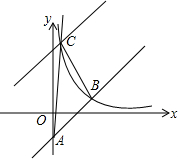 如图,已知直线y=x+a与y轴相交于点A,与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点B(-a+1,a+4).
如图,已知直线y=x+a与y轴相交于点A,与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点B(-a+1,a+4).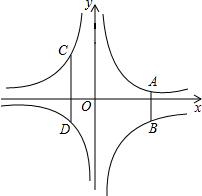 如图,已知点A,D在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点B,C在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥y轴,AB,CD在x轴的两侧,AB=1,CD=2,AB与CD的距离为3,则a-b的值是2.
如图,已知点A,D在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点B,C在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥y轴,AB,CD在x轴的两侧,AB=1,CD=2,AB与CD的距离为3,则a-b的值是2.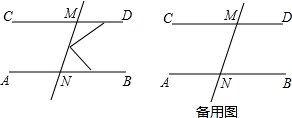 如图1,直线AB∥CD,P是截线MN上的一点.
如图1,直线AB∥CD,P是截线MN上的一点.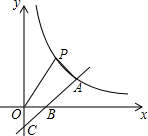 如图,一次函数y=x+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(2,m),与x轴、y轴分别交于B、C两点,C点坐标为(0,-1).
如图,一次函数y=x+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(2,m),与x轴、y轴分别交于B、C两点,C点坐标为(0,-1).