题目内容
19.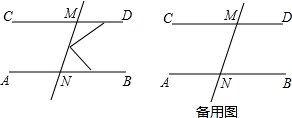 如图1,直线AB∥CD,P是截线MN上的一点.
如图1,直线AB∥CD,P是截线MN上的一点.(1)若∠MNB=45°,∠MDP=20°,求∠MPD的度数;
(2)当点P在直线MN上运动时,∠CDP与∠ABP的平分线交于Q,请直接写出∠Q、∠DPB之间的数量关系.
分析 (1)作PE∥AB,则AB∥CD∥PE,由平行线的性质得出∠MPE=∠MNB=45°,∠1=∠MDP=20°,即可得出结果;
(2)作QE∥CD,PF∥CD,则QE∥AB,EF∥AB,由平行线的性质得出∠CDQ=∠DQE①,∠ABQ=∠BQE②,得出∠BQD=∠1+∠3,同理:∠BPD=∠CDP+∠ABP,再由角平分线的定义即可得出结果.
解答 解: (1)作PE∥AB,如图1所示:
(1)作PE∥AB,如图1所示:
∵AB∥CD,
∴AB∥CD∥PE,
∴∠MPE=∠MNB=45°,∠1=∠MDP=20°,
∴∠MPD=45°-20°=25°;
(2)∠DPB=2∠BQD;理由如下:
作QE∥CD,PF∥CD,如图2所示:
则QE∥AB,EF∥AB,
∴∠CDQ=∠DQE①,∠ABQ=∠BQE②,
①+②得:∠BQD=∠CDQ+∠ABQ,
同理:∠BPD=∠CDP+∠ABP,
∵∠CDP与∠ABP的平分线交于Q,
∴∠CDQ=∠∠1=$\frac{1}{2}$∠CDP,∠3=$\frac{1}{2}$∠ABP,
∴∠DPB=2∠BQD.
点评 本题考查了平行线的性质、角平分线的定义;熟练掌握平行线的性质是解决问题的关键,注意辅助线的作法.

练习册系列答案
相关题目
7.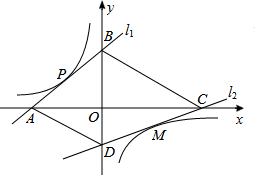 如图,直线l1解析式为y=x+2,且与坐标轴分别交于A、B两点,与双曲线交于点P(-1,1).点M是双曲线在第四象限上的一点,过点M的直线l2与双曲线只有一个公共点,并与坐标轴分别交于点C、点D,当四边形ABCD的面积取最小值时,则点M的坐标为( )
如图,直线l1解析式为y=x+2,且与坐标轴分别交于A、B两点,与双曲线交于点P(-1,1).点M是双曲线在第四象限上的一点,过点M的直线l2与双曲线只有一个公共点,并与坐标轴分别交于点C、点D,当四边形ABCD的面积取最小值时,则点M的坐标为( )
 如图,直线l1解析式为y=x+2,且与坐标轴分别交于A、B两点,与双曲线交于点P(-1,1).点M是双曲线在第四象限上的一点,过点M的直线l2与双曲线只有一个公共点,并与坐标轴分别交于点C、点D,当四边形ABCD的面积取最小值时,则点M的坐标为( )
如图,直线l1解析式为y=x+2,且与坐标轴分别交于A、B两点,与双曲线交于点P(-1,1).点M是双曲线在第四象限上的一点,过点M的直线l2与双曲线只有一个公共点,并与坐标轴分别交于点C、点D,当四边形ABCD的面积取最小值时,则点M的坐标为( )| A. | (1,-1) | B. | (2,-$\frac{1}{2}$) | C. | (3,-$\frac{1}{3}$) | D. | 不能确定 |
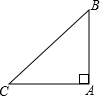 如图,在Rt△ABC中,∠BAC=90°,AB=AC.
如图,在Rt△ABC中,∠BAC=90°,AB=AC.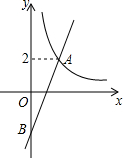 如图,在平面直角坐标系xOy中,双曲线y=$\frac{4}{x}$(x>0)与直线y=kx-k的交点为A(m,2).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{4}{x}$(x>0)与直线y=kx-k的交点为A(m,2).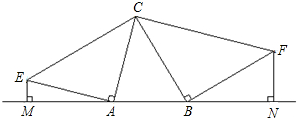 如图,锐角△ABC分别以A、B为直角顶点,向△ABC外作等腰直角三角形ACE和等腰直角三角形BCF,再分别过点E、F作边AB所在直线的垂线,垂足为M,N.
如图,锐角△ABC分别以A、B为直角顶点,向△ABC外作等腰直角三角形ACE和等腰直角三角形BCF,再分别过点E、F作边AB所在直线的垂线,垂足为M,N.