题目内容
14．在二次函数y=ax2+bx+c中，若a＞0，b2-4ac=0，则它的图象可能是（ ）| A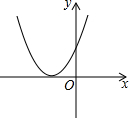． |  | B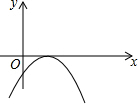． |  | C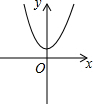． |  | D． |  |
分析 根据二次函数图象的特点，由a＞0，可知抛物线的开口方向，由b2-4ac=0，可知该函数图象与x轴的交点个数．
解答 解：在二次函数y=ax2+bx+c中，若a＞0，则该抛物线的开口向上，b2-4ac=0，说明该抛物线的图象与x轴只有一个交点，
故选A．
点评 本题考查二次函数的图象，解题的关键是明确二次函数图象的特点，明确a的正负决定抛物线的开口方向，b2-4ac=0决定抛物线与x轴的交点个数．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
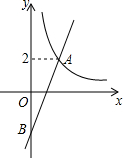如图，在平面直角坐标系xOy中，双曲线y=$\frac{4}{x}$（x＞0）与直线y=kx-k的交点为A（m，2）．
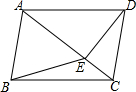如图，在四边形ABCD中，AB∥CD，∠ABC=∠ADC，DE垂直于对角线AC，垂足是E，连接BE．
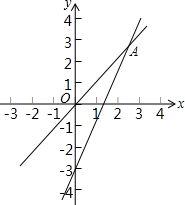已知一个正比例函数与一个一次函数的图象交于点A（3，4），且0A=0B
6．
（1）画出函数y=-$\frac{6}{x}$（x＜0）的图象：
列表：
描点并连线．
（2）从图象可以看出，曲线从左向右依次升高，当x由小变大时，y=-$\frac{6}{x}$（x＜0）随之变大．
（1）画出函数y=-$\frac{6}{x}$（x＜0）的图象：列表：
| x | … | -6 | -5 | -4 | -3 | -2 | -1 | … |
| y | … | … |
（2）从图象可以看出，曲线从左向右依次升高，当x由小变大时，y=-$\frac{6}{x}$（x＜0）随之变大．
3．若直线y=kx+b（k＜0，b＞0）的大致图象为（ ）
| A． |  | B． |  | C． |  | D． |  |
