题目内容
4.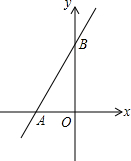 如图,平面直角坐标系中,点O为坐标原点,一次函数的图象过点(-1,4)与点(3,12).
如图,平面直角坐标系中,点O为坐标原点,一次函数的图象过点(-1,4)与点(3,12).(1)求这个一次函数的解析式;
(2)若这个一次函数图象与x轴交于点A,与y轴交于点B,求三角形AOB的面积;
(3)若点M是这个一次函数图象上一点,MN⊥x轴于点N,点P在y轴上,当以点M、N、P顶点的三角形是等腰直角三角形时,求点M坐标.
分析 (1)利用待定系数法求一次函数解析式为;
(2)先利用坐标轴上点的坐标特征确定A点和B点坐标,然后根据三角形面积公式计算;
(3)如图,设M(t,2t+6),分类讨论:当∠NMP=90°或∠MNP=90°,根据等腰直角三角形的性质得|t|=|2t+6|;当∠MPN=90°时,利等腰直角三角形斜边上的高等于斜边得一半得到|t|=$\frac{1}{2}$|2t+6|,然后分别解关于t的方程即可得到M点的坐标.
解答 解:(1)设一次函数解析式为y=kx+b,
根据题意得$\left\{\begin{array}{l}{-k+b=4}\\{3k+b=12}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=2}\\{b=6}\end{array}\right.$,
所以一次函数解析式为y=2x+6;
(2)当x=0时,y=2x+6=6,则B(0,6),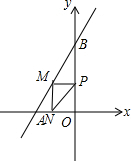
当y=0时,2x+6=0,解得x=-3,则A(-3,0),
所以三角形AOB的面积=$\frac{1}{2}$×3×6=9;
(3)如图,设M(t,2t+6),
当∠NMP=90°或∠MNP=90°,则|t|=|2t+6|,解得t=-2或t=-6,此时M点坐标为(-2,2)或(-6,-6);
当∠MPN=90°时,|t|=$\frac{1}{2}$|2t+6|,解得t=-$\frac{3}{2}$,此时M点坐标为(-$\frac{3}{2}$,3),
综上所述,满足条件的M点坐标为(-2,2)或(-6,-6)或(-$\frac{3}{2}$,3).
点评 本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;再将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;然后解方程或方程组,求出待定系数的值,进而写出函数解析式.灵活运用坐标与图形性质和等腰直角三角形的性质是解决(3)小题的关键.



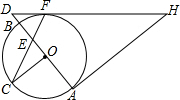 如图,在⊙O中,AB为直径,OC⊥AB,弦CF与OB交于点E,过点F,A分别作⊙O的切线交于点H,且HF与AB的延长线交于点D.
如图,在⊙O中,AB为直径,OC⊥AB,弦CF与OB交于点E,过点F,A分别作⊙O的切线交于点H,且HF与AB的延长线交于点D.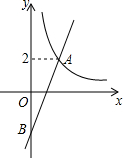 如图,在平面直角坐标系xOy中,双曲线y=$\frac{4}{x}$(x>0)与直线y=kx-k的交点为A(m,2).
如图,在平面直角坐标系xOy中,双曲线y=$\frac{4}{x}$(x>0)与直线y=kx-k的交点为A(m,2).