题目内容
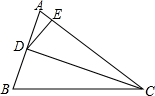 如图,已知CD是△ABC中∠ACB的角平分线,E是AC上的一点,且CD2=BC•CE,AD=6,AE=4.
如图,已知CD是△ABC中∠ACB的角平分线,E是AC上的一点,且CD2=BC•CE,AD=6,AE=4.(1)求证:△BCD∽△DCE;
(2)求证:△ADE∽△ACD;
(3)求CE的长.
考点:相似三角形的判定与性质
专题:
分析:(1)根据两边对应成比例,且夹角相等的两个三角形相似,可得答案;
(2)根据两个角对应相等的两个三角形相似,可得答案;
(3)根据两个三角形相似,对应边成比例,可得答案.
(2)根据两个角对应相等的两个三角形相似,可得答案;
(3)根据两个三角形相似,对应边成比例,可得答案.
解答:(1)证明:CD是△ABC中∠ACB的角平分线,
∴∠BCD=∠DCE.
∵CD2=BC•CE,
∴
=
,
∴△BCD∽△DCE(两边对应成比例,且夹角相等的两个三角形相似);
(2)证明:∵△BCD∽△DCE,
∴∠EDC=∠DBC(相似三角形的对应角相等).
∵∠ADC=∠DBC+∠DCB(三角形的外角等于与它不相邻的两个内角的和),
∠ADC=∠ADE+∠EDC,
∴∠ADE=∠ACD.
∠A=∠A,
∴△ADE∽△ACD(两个角对应相等的两个三角形相似);
(3)解:∵△ADE∽△ACD,
∴
=
,
=
AC=9,
CE=AC-AE=9-4=5.
∴∠BCD=∠DCE.
∵CD2=BC•CE,
∴
| CD |
| BC |
| CE |
| CD |
∴△BCD∽△DCE(两边对应成比例,且夹角相等的两个三角形相似);
(2)证明:∵△BCD∽△DCE,
∴∠EDC=∠DBC(相似三角形的对应角相等).
∵∠ADC=∠DBC+∠DCB(三角形的外角等于与它不相邻的两个内角的和),
∠ADC=∠ADE+∠EDC,
∴∠ADE=∠ACD.
∠A=∠A,
∴△ADE∽△ACD(两个角对应相等的两个三角形相似);
(3)解:∵△ADE∽△ACD,
∴
| AD |
| AC |
| AE |
| AD |
| 6 |
| AC |
| 4 |
| 6 |
AC=9,
CE=AC-AE=9-4=5.
点评:本题考查了相似三角形的判定与性质,两边对应成比例且夹角相等的两个三角形相似,两角对应相等的两个三角形相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列多项式属于完全平方式的是( )
| A、x2-2x+4 | ||
B、x2+x+
| ||
| C、x2-xy+y2 | ||
| D、4x2-4x-1 |
 已知Y1,Y2,Y3分别表示二次函数、反比例函数和一次函数的三个函数值,它们的交点分别是A(-1,-2)、B(2,1)和C(
已知Y1,Y2,Y3分别表示二次函数、反比例函数和一次函数的三个函数值,它们的交点分别是A(-1,-2)、B(2,1)和C(| 2 |
| 3 |
| A、当x<-1时,M=Y1 |
| B、当-1<x<0时,Y2<Y3<Y1 |
| C、当0≤x≤2时,M的最大值是1,无最小值 |
| D、当x≥2时,M最大值是1,无最小值 |

 如图,已知矩形ABCD中,E是AD上的一点,过点E作EF⊥EC 交边AB于点F,交CB的延长线于点G,且EF=EC.
如图,已知矩形ABCD中,E是AD上的一点,过点E作EF⊥EC 交边AB于点F,交CB的延长线于点G,且EF=EC. 如图所示,在矩形ABCD中,AB=6,BC=8,将矩形折叠,使点C与点A重合,折痕为EF,再展平,EF与AC相交于点O,连接AF,CE,求折痕EF的长.
如图所示,在矩形ABCD中,AB=6,BC=8,将矩形折叠,使点C与点A重合,折痕为EF,再展平,EF与AC相交于点O,连接AF,CE,求折痕EF的长. 如图,已知AB∥CD,请探索图形中∠P与∠A,∠C的关系,并说明理由.
如图,已知AB∥CD,请探索图形中∠P与∠A,∠C的关系,并说明理由.