题目内容
 如图,已知矩形ABCD中,E是AD上的一点,过点E作EF⊥EC 交边AB于点F,交CB的延长线于点G,且EF=EC.
如图,已知矩形ABCD中,E是AD上的一点,过点E作EF⊥EC 交边AB于点F,交CB的延长线于点G,且EF=EC.(1)求证:CD=AE;
(2)若DE=4cm,矩形ABCD的周长为 32cm,求CG的长.
考点:相似三角形的判定与性质,全等三角形的判定与性质,矩形的性质
专题:
分析:(1)若要证明CD=AE,则可证明两条线段所在的三角形全等即可;
(2)由AD∥BC可证△AEF∽△BGF,根据相似三角形的性质:对应边的比值相等可求出BG的长,进而求出CG的长.
(2)由AD∥BC可证△AEF∽△BGF,根据相似三角形的性质:对应边的比值相等可求出BG的长,进而求出CG的长.
解答:(1)证明:在Rt△AEF和Rt△DEC中,
∵EF⊥CE,
∴∠FEC=90°.
∴∠AEF+∠DEC=90°,而∠ECD+∠DEC=90°,
∴∠AEF=∠ECD.
又∠FAE=∠EDC=90°,EF=EC,
在Rt△AEF和Rt△DCE中,
,
∴Rt△AEF≌Rt△DCE(AAS).
∴AE=CD.
(2)∵AD=AE+4,
∵矩形ABCD的周长为32 cm,
∴2(AE+AE+4)=32..
解得 AE=6.
∴AF=4,BF=2.
由AD∥BC可证△AEF∽△BGF.
∴
=
=2.
∴BG=3.
∴CG=13.
∵EF⊥CE,
∴∠FEC=90°.
∴∠AEF+∠DEC=90°,而∠ECD+∠DEC=90°,
∴∠AEF=∠ECD.
又∠FAE=∠EDC=90°,EF=EC,

在Rt△AEF和Rt△DCE中,
|
∴Rt△AEF≌Rt△DCE(AAS).
∴AE=CD.
(2)∵AD=AE+4,
∵矩形ABCD的周长为32 cm,
∴2(AE+AE+4)=32..
解得 AE=6.
∴AF=4,BF=2.
由AD∥BC可证△AEF∽△BGF.
∴
| AE |
| BG |
| AF |
| BF |
∴BG=3.
∴CG=13.
点评:本题考查了矩形的性质、全等三角形的判定和性质以及相似三角形的判定和性质,题目的综合性较强,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2011年4月28日西安世园会举办以来,入园参观人数已达1280万人,这个数用科学记数法可表示为( )
| A、1.28×108人 |
| B、12.8×107人 |
| C、1.28×107人 |
| D、0.128×108人 |
已知两圆半径r1、r2分别是方程x2-5x+4=0的两根,两圆的圆心距为5,则两圆的位置关系是( )
| A、相交 | B、内切 | C、外切 | D、外离 |
 如图,点O为正方形ABCD的中心,AB=12,点E在BC边上,以AE为边作等边三角形AEF.
如图,点O为正方形ABCD的中心,AB=12,点E在BC边上,以AE为边作等边三角形AEF. 已知矩形ABCD中,AB=60cm,BC=40cm,动点P从A点出发,沿着矩形的边自A→B→C→D运动到点D,速度为1m/s,设运动时间为 t(s),线段AP的长为y(cm),求此函数的解析式.
已知矩形ABCD中,AB=60cm,BC=40cm,动点P从A点出发,沿着矩形的边自A→B→C→D运动到点D,速度为1m/s,设运动时间为 t(s),线段AP的长为y(cm),求此函数的解析式. 如图,直线y=x+b与二次函数y=x2+x-4交于A、B两点,与y轴交于点C,是否存在这样的b,使得△AOB是以AB为斜边的直角三角形?若存在,求出b;若不存在,说明理由.
如图,直线y=x+b与二次函数y=x2+x-4交于A、B两点,与y轴交于点C,是否存在这样的b,使得△AOB是以AB为斜边的直角三角形?若存在,求出b;若不存在,说明理由.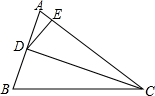 如图,已知CD是△ABC中∠ACB的角平分线,E是AC上的一点,且CD2=BC•CE,AD=6,AE=4.
如图,已知CD是△ABC中∠ACB的角平分线,E是AC上的一点,且CD2=BC•CE,AD=6,AE=4.